
Question Number 165194 by mnjuly1970 last updated on 27/Jan/22
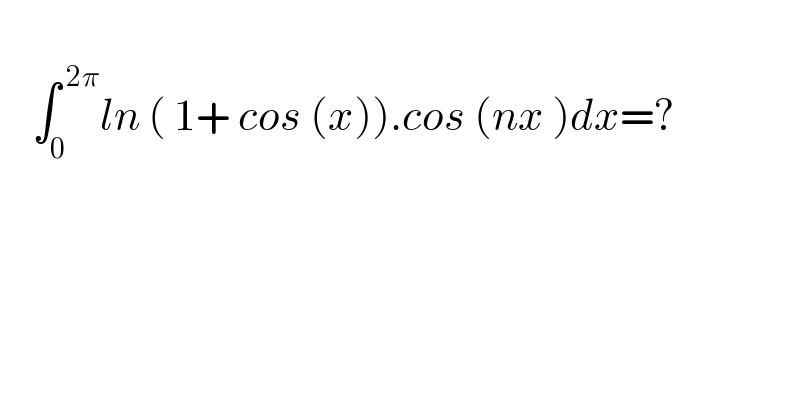
$$ \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} {ln}\:\left(\:\mathrm{1}+\:{cos}\:\left({x}\right)\right).{cos}\:\left({nx}\:\right){dx}=? \\ $$
Answered by mindispower last updated on 27/Jan/22

$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right){cos}\left({nx}\right){dx} \\ $$$${x}=\mathrm{2}{y} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left({y}\right)\right){cos}\left(\mathrm{2}{ny}\right){dy} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left({y}\right)\right){cos}\left(\mathrm{2}{ny}\right){dy}+\mathrm{2}\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} {ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left({y}\right)\right){cos}\left(\mathrm{2}{ny}\right){dy} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{ny}\right){ln}\left(\mathrm{2}{cos}^{\mathrm{2}} \left({y}\right)\right){dy} \\ $$$$=\mathrm{4}{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{ny}\right)+\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{ny}\right){ln}\left({cos}\left({y}\right)\right){dy} \\ $$$$\left.=−\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}{cos}\left(\mathrm{2}{ky}\right){cos}\left(\mathrm{2}{ny}\right){dy}−\mathrm{8}{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\mathrm{2}{ny}\right){dy} \\ $$$$=−\mathrm{4}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}\left({k}+{n}\right){x}\right)+{cos}\left(\mathrm{2}\left({k}−{n}\right){x}\right){dx} \\ $$$${n}\in\mathbb{N},{k}+{n}\neq\mathrm{0};\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}\left({k}+{n}\right){x}\right){dx}=\mathrm{0} \\ $$$$=−\mathrm{4}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}\left({k}−{n}\right){x}\right){dx}=−\mathrm{4}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$$=−\mathrm{2}\pi\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}=\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\pi,\forall{n}\geqslant\mathrm{1} \\ $$$${n}=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {ln}\left(+{cos}\left({x}\right)\right){dx}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {ln}\left(\mathrm{2}\right)+{ln}\left({cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right){dx} \\ $$$$=\mathrm{2}\pi{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\pi} {ln}\left({cos}^{\mathrm{2}} \left({x}\right)\right)\mathrm{2}{dx} \\ $$$$=\mathrm{2}\pi{ln}\left(\mathrm{2}\right)+\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$=−\mathrm{2}\pi{ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {ln}\left(\mathrm{1}+{cos}\left({x}\right)\right){cos}\left({x}\right){dx}=\begin{cases}{−\mathrm{2}\pi{ln}\left(\mathrm{2}\right)\:,{n}=\mathrm{0}}\\{\mathrm{2}\pi.\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}};{n}\geqslant\mathrm{1}}\end{cases} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 27/Jan/22
$${very}\:{nice}\:\:..\:{really}\:{very}\:{nice}\:{solution} \\ $$$${sir}\:{power}\:\:{thanks}\:{alot} \\ $$
Commented by mindispower last updated on 27/Jan/22
$${thanxSir}\:{withe}\:{Pleasur} \\ $$$${Have}\:{a}\:{nice}\:{Day} \\ $$
Answered by aleks041103 last updated on 27/Jan/22
![IBP: I_n =[(1/n)ln(1+cos(x))sin(nx)]_0 ^(2π) +(1/n)∫_0 ^(2π) ((sin(x)sin(nx))/(1+cos(x)))dx ⇒I_n =(1/n)∫_0 ^(2π) ((sin(x)sin(nx))/(1+cos(x)))dx let z=e^(ix) ⇒dz=ie^(ix) dx=izdx⇒dx=(dz/(iz)) sin(x)=((e^(ix) −e^(−ix) )/(2i))=((z^2 −1)/(2iz)) sin(nx)=((z^(2n) −1)/(2iz^n )) cos(x)=((e^(ix) +e^(−ix) )/2)=((z^2 +1)/(2z)) ⇒((sin(x)sin(nx))/(1+cos(x)))dx=(((z^2 −1)(z^(2n) −1))/(−4iz^(n+2) (1+((z^2 +1)/(2z)))))dz= =i(((z−1)(z+1)(z^(2n) −1))/(2z^(n+1) (z+1)^2 ))dz=(i/2) (((z−1)(z^(2n) −1))/(z^(n+1) (z+1)))dz Also when x∈[0,2π], z=e^(ix) ∈Γ:∣z∣=1. ⇒I_n =(i/(2n))∮_Γ (((z−1)(z^(2n) −1))/(z^(n+1) (z+1)))dz=(i/(2n))∮_Γ f(z)dz This can be evaluated using the Residue theorem. Poles of f(z): 1)z=−1 lim_(z→−1) (((z−1)(z^(2n) −1))/(z^(n+1) (z+1)))=2(−1)^n lim_(z→−1) ((z^(2n) −1)/(z+1))= =^(l′H) 2(−1)^n lim_(z→−1) ((2nz^(2n−1) )/1)=4n(−1)^(n+1) ↛±∞ ⇒z=−1 is not a pole! 2) z=0 − obv. a pole of (n+1)−th order. ⇒∮_Γ f(z)dz=2πiRes(f,0) ⇒I_n =−(π/n)Res(f,0) Res(f,0)=(1/(n!))lim_(z→0) [(d^n /dz^n )(z^(n+1) f(z))]= =(1/(n!))lim_(z→0) [(d^n /dz^n )((((z−1)(z^(2n) −1))/((z+1))))] (((z−1)(z^(2n) −1))/((z+1)))=(z^(2n) −1)((z−1)/(z+1))= =(z^(2n) −1)(1−(2/(z+1)))= =z^(2n) +(2/(z+1))−1−((2z^(2n) )/(z+1)) ⇒(d^n /dz^n )((((z−1)(z^(2n) −1))/((z+1))))= =(((2n)!)/(n!))z^n +2(−1)^n n!(1/((z+1)^(n+1) ))−2(d^n /dz^n )((z^(2n) /(z+1))) ⇒Res(0,f)=2(−1)^n −(2/(n!)) (d^n /dz^n )((z^(2n) /(z+1)))_(z=0) Since we want (d^n /dz^n )((z^(2n) /(z+1))) at z=0 (∣z∣=0<1) we can use (1/(1+z))=Σ_(i=0) ^∞ (−z)^i ⇒ (d^n /dz^n )((z^(2n) /(z+1)))_(z=0) = (d^n /dz^n )(Σ_(i=0) ^∞ (−z)^(i+2n) )_(z=0) = =Σ_(i=0) ^∞ (((2n+i)!)/((n+i)!))((−z)^(i+n) )_(z=0) since for i≥0 and n≥1, i+n≥1 then ((−z)^(i+n) )_(z=0) =0 ⇒(d^n /dz^n )((z^(2n) /(z+1)))_(z=0) = 0 ⇒Res(0,f)=2(−1)^n ⇒I_n =((2(−1)^(n+1) π)/n)](Q165205.png)
$${IBP}: \\ $$$${I}_{{n}} =\left[\frac{\mathrm{1}}{{n}}{ln}\left(\mathrm{1}+{cos}\left({x}\right)\right){sin}\left({nx}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} +\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{sin}\left({x}\right){sin}\left({nx}\right)}{\mathrm{1}+{cos}\left({x}\right)}{dx} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{sin}\left({x}\right){sin}\left({nx}\right)}{\mathrm{1}+{cos}\left({x}\right)}{dx} \\ $$$${let}\:{z}={e}^{{ix}} \\ $$$$\Rightarrow{dz}={ie}^{{ix}} {dx}={izdx}\Rightarrow{dx}=\frac{{dz}}{{iz}} \\ $$$${sin}\left({x}\right)=\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}}=\frac{{z}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{iz}} \\ $$$${sin}\left({nx}\right)=\frac{{z}^{\mathrm{2}{n}} −\mathrm{1}}{\mathrm{2}{iz}^{{n}} } \\ $$$${cos}\left({x}\right)=\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}}=\frac{{z}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{z}} \\ $$$$\Rightarrow\frac{{sin}\left({x}\right){sin}\left({nx}\right)}{\mathrm{1}+{cos}\left({x}\right)}{dx}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{−\mathrm{4}{iz}^{{n}+\mathrm{2}} \left(\mathrm{1}+\frac{{z}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{z}}\right)}{dz}= \\ $$$$={i}\frac{\left({z}−\mathrm{1}\right)\left({z}+\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{\mathrm{2}{z}^{{n}+\mathrm{1}} \left({z}+\mathrm{1}\right)^{\mathrm{2}} }{dz}=\frac{{i}}{\mathrm{2}}\:\frac{\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{{z}^{{n}+\mathrm{1}} \left({z}+\mathrm{1}\right)}{dz} \\ $$$${Also}\:{when}\:{x}\in\left[\mathrm{0},\mathrm{2}\pi\right],\:{z}={e}^{{ix}} \in\Gamma:\mid{z}\mid=\mathrm{1}. \\ $$$$\Rightarrow{I}_{{n}} =\frac{{i}}{\mathrm{2}{n}}\underset{\Gamma} {\oint}\frac{\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{{z}^{{n}+\mathrm{1}} \left({z}+\mathrm{1}\right)}{dz}=\frac{{i}}{\mathrm{2}{n}}\underset{\Gamma} {\oint}{f}\left({z}\right){dz} \\ $$$${This}\:{can}\:{be}\:{evaluated}\:{using}\:{the} \\ $$$${Residue}\:{theorem}. \\ $$$${Poles}\:{of}\:{f}\left({z}\right): \\ $$$$\left.\mathrm{1}\right){z}=−\mathrm{1} \\ $$$$\underset{{z}\rightarrow−\mathrm{1}} {{lim}}\frac{\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{{z}^{{n}+\mathrm{1}} \left({z}+\mathrm{1}\right)}=\mathrm{2}\left(−\mathrm{1}\right)^{{n}} \underset{{z}\rightarrow−\mathrm{1}} {{lim}}\frac{{z}^{\mathrm{2}{n}} −\mathrm{1}}{{z}+\mathrm{1}}= \\ $$$$\overset{{l}'{H}} {=}\mathrm{2}\left(−\mathrm{1}\right)^{{n}} \underset{{z}\rightarrow−\mathrm{1}} {{lim}}\frac{\mathrm{2}{nz}^{\mathrm{2}{n}−\mathrm{1}} }{\mathrm{1}}=\mathrm{4}{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \nrightarrow\pm\infty \\ $$$$\Rightarrow{z}=−\mathrm{1}\:{is}\:{not}\:{a}\:{pole}! \\ $$$$\left.\mathrm{2}\right)\:{z}=\mathrm{0}\:−\:{obv}.\:{a}\:{pole}\:{of}\:\left({n}+\mathrm{1}\right)−{th}\:{order}. \\ $$$$\Rightarrow\underset{\Gamma} {\oint}{f}\left({z}\right){dz}=\mathrm{2}\pi{iRes}\left({f},\mathrm{0}\right) \\ $$$$\Rightarrow{I}_{{n}} =−\frac{\pi}{{n}}{Res}\left({f},\mathrm{0}\right) \\ $$$$ \\ $$$${Res}\left({f},\mathrm{0}\right)=\frac{\mathrm{1}}{{n}!}\underset{{z}\rightarrow\mathrm{0}} {{lim}}\left[\frac{{d}^{{n}} }{{dz}^{{n}} }\left({z}^{{n}+\mathrm{1}} {f}\left({z}\right)\right)\right]= \\ $$$$=\frac{\mathrm{1}}{{n}!}\underset{{z}\rightarrow\mathrm{0}} {{lim}}\left[\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{\left({z}+\mathrm{1}\right)}\right)\right] \\ $$$$\frac{\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{\left({z}+\mathrm{1}\right)}=\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)\frac{{z}−\mathrm{1}}{{z}+\mathrm{1}}= \\ $$$$=\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{{z}+\mathrm{1}}\right)= \\ $$$$={z}^{\mathrm{2}{n}} +\frac{\mathrm{2}}{{z}+\mathrm{1}}−\mathrm{1}−\frac{\mathrm{2}{z}^{\mathrm{2}{n}} }{{z}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{\left({z}−\mathrm{1}\right)\left({z}^{\mathrm{2}{n}} −\mathrm{1}\right)}{\left({z}+\mathrm{1}\right)}\right)= \\ $$$$=\frac{\left(\mathrm{2}{n}\right)!}{{n}!}{z}^{{n}} +\mathrm{2}\left(−\mathrm{1}\right)^{{n}} {n}!\frac{\mathrm{1}}{\left({z}+\mathrm{1}\right)^{{n}+\mathrm{1}} }−\mathrm{2}\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{{z}^{\mathrm{2}{n}} }{{z}+\mathrm{1}}\right) \\ $$$$\Rightarrow{Res}\left(\mathrm{0},{f}\right)=\mathrm{2}\left(−\mathrm{1}\right)^{{n}} −\frac{\mathrm{2}}{{n}!}\:\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{{z}^{\mathrm{2}{n}} }{{z}+\mathrm{1}}\right)_{{z}=\mathrm{0}} \\ $$$${Since}\:{we}\:{want}\:\:\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{{z}^{\mathrm{2}{n}} }{{z}+\mathrm{1}}\right)\:{at}\:{z}=\mathrm{0}\:\left(\mid{z}\mid=\mathrm{0}<\mathrm{1}\right)\:{we}\:{can} \\ $$$${use}\:\frac{\mathrm{1}}{\mathrm{1}+{z}}=\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−{z}\right)^{{i}} \\ $$$$\Rightarrow\:\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{{z}^{\mathrm{2}{n}} }{{z}+\mathrm{1}}\right)_{{z}=\mathrm{0}} =\:\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−{z}\right)^{{i}+\mathrm{2}{n}} \right)_{{z}=\mathrm{0}} = \\ $$$$=\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}{n}+{i}\right)!}{\left({n}+{i}\right)!}\left(\left(−{z}\right)^{{i}+{n}} \right)_{{z}=\mathrm{0}} \\ $$$${since}\:{for}\:{i}\geqslant\mathrm{0}\:{and}\:{n}\geqslant\mathrm{1},\:{i}+{n}\geqslant\mathrm{1}\:{then} \\ $$$$\left(\left(−{z}\right)^{{i}+{n}} \right)_{{z}=\mathrm{0}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{d}^{{n}} }{{dz}^{{n}} }\left(\frac{{z}^{\mathrm{2}{n}} }{{z}+\mathrm{1}}\right)_{{z}=\mathrm{0}} =\:\mathrm{0} \\ $$$$\Rightarrow{Res}\left(\mathrm{0},{f}\right)=\mathrm{2}\left(−\mathrm{1}\right)^{{n}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \pi}{{n}} \\ $$$$ \\ $$
Commented by mindispower last updated on 28/Jan/22

$${nice}\:{Solution}\:{Sir} \\ $$
