Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 85568 by jagoll last updated on 23/Mar/20

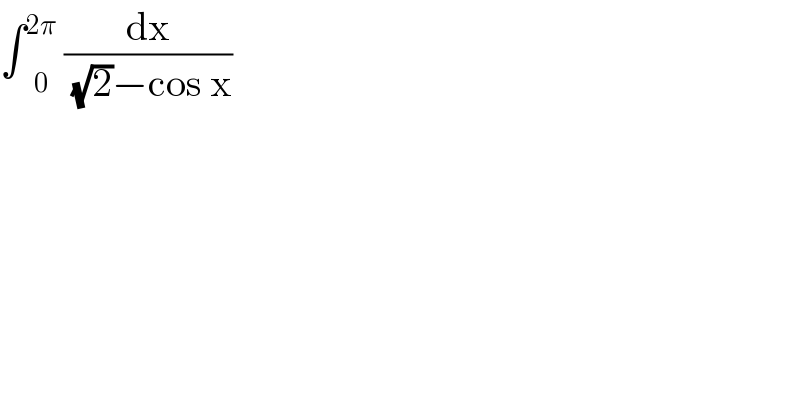
∫ _0 ^(2π) (dx/((√2)−cos x))

$$\int\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\:}}\:\frac{\mathrm{dx}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\mathrm{x}} \\ $$

Commented by jagoll last updated on 23/Mar/20

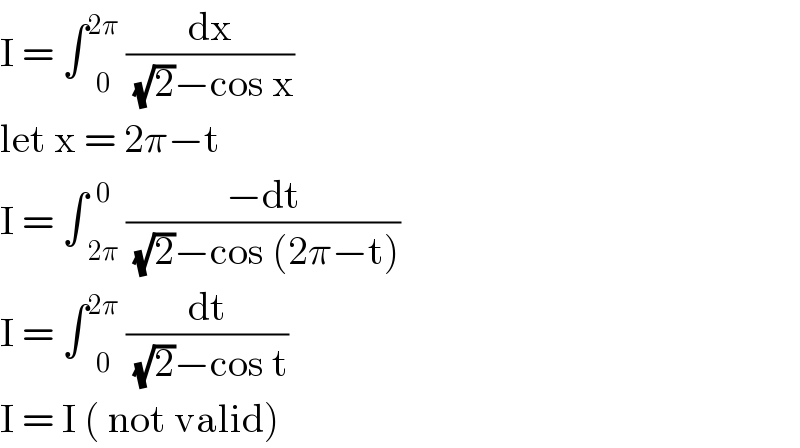
I = ∫ _0 ^(2π) (dx/((√2)−cos x)) let x = 2π−t I = ∫ _(2π) ^0 ((−dt)/((√2)−cos (2π−t))) I = ∫ _0 ^(2π) (dt/((√2)−cos t)) I = I ( not valid)

$$\mathrm{I}\:=\:\int\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\:}}\:\frac{\mathrm{dx}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\mathrm{x}} \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{2}\pi−\mathrm{t}\: \\ $$$$\mathrm{I}\:=\:\int\underset{\mathrm{2}\pi} {\overset{\mathrm{0}} {\:}}\:\frac{−\mathrm{dt}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\left(\mathrm{2}\pi−\mathrm{t}\right)} \\ $$$$\mathrm{I}\:=\:\int\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\:}}\:\frac{\mathrm{dt}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\mathrm{t}}\: \\ $$$$\mathrm{I}\:=\:\mathrm{I}\:\left(\:\mathrm{not}\:\mathrm{valid}\right)\: \\ $$

Commented by mathmax by abdo last updated on 23/Mar/20

A =∫_0 ^(2π) (dx/((√2)−cosx)) ⇒ A =∫_0 ^(2π) (dx/((√2)−((e^(ix) +e^(−ix) )/2))) =∫_0 ^(2π) ((2dx)/(2(√2)−e^(ix) −e^(−ix) )) =_(e^(ix) =z) ∫_(∣z∣=1) (2/(2(√2)−z−z^(−1) )) (dz/(iz)) =∫_(∣z∣=1) ((−2idz)/(2(√2)z−z^2 −1)) =∫_(∣z∣=1) ((2i dz)/(z^2 −2(√2)z +1)) =∫_(∣z∣=1) ϕ(z)dz with ϕ(z)=((2i)/(z^2 −2(√2)z +1)) poles of ϕ? z^2 −2(√2)z +1 =0 →Δ^′ =2−1 =1 ⇒z_1 =1+(√2) and z_2 =−1+(√2) ⇒ϕ(z)=((2i)/((z−z_1 )(z−z_2 ))) ∣z_1 ∣−1 =1+(√2)−1 >0 (out of circle) ∣z_2 ∣−1 =∣(√2)−1∣−1 =(√2)−2 <0 ⇒ ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_2 ) =2iπ ×((2i)/((z_2 −z_1 ))) =((−4π)/(−2)) =2π ⇒A =2π

$${A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\sqrt{\mathrm{2}}−{cosx}}\:\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\sqrt{\mathrm{2}}−\frac{{e}^{{ix}} \:+{e}^{−{ix}} }{\mathrm{2}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{2}{dx}}{\mathrm{2}\sqrt{\mathrm{2}}−{e}^{{ix}} −{e}^{−{ix}} }\:=_{{e}^{{ix}} ={z}} \:\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}−{z}−{z}^{−\mathrm{1}} }\:\frac{{dz}}{{iz}} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\frac{−\mathrm{2}{idz}}{\mathrm{2}\sqrt{\mathrm{2}}{z}−{z}^{\mathrm{2}} −\mathrm{1}}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{2}{i}\:{dz}}{{z}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{z}\:+\mathrm{1}}\:\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz} \\ $$$${with}\:\varphi\left({z}\right)=\frac{\mathrm{2}{i}}{{z}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{z}\:+\mathrm{1}}\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{z}\:+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta^{'} =\mathrm{2}−\mathrm{1}\:=\mathrm{1}\:\Rightarrow{z}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:{and}\:{z}_{\mathrm{2}} =−\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\varphi\left({z}\right)=\frac{\mathrm{2}{i}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$$\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\mathrm{1}+\sqrt{\mathrm{2}}−\mathrm{1}\:>\mathrm{0}\:\:\left({out}\:{of}\:{circle}\right) \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mid\sqrt{\mathrm{2}}−\mathrm{1}\mid−\mathrm{1}\:=\sqrt{\mathrm{2}}−\mathrm{2}\:<\mathrm{0}\:\:\Rightarrow \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{2}} \right)\:=\mathrm{2}{i}\pi\:×\frac{\mathrm{2}{i}}{\left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)}\:=\frac{−\mathrm{4}\pi}{−\mathrm{2}}\:=\mathrm{2}\pi \\ $$$$\Rightarrow{A}\:=\mathrm{2}\pi \\ $$

Answered by mind is power last updated on 23/Mar/20

=∫_0 ^π (dx/((√2)−cos(x)))+∫_π ^(2π) (dx/((√2)−cos(x))) t=π+x in 2nd⇒ =∫_0 ^π (dx/((√2)−cos(x)))+(dx/((√2)+cos(x))) =∫_0 ^π ((2(√2)dx)/(2−cos^2 (x)))=2(√2)∫_0 ^(π/2) (dx/(2−cos^2 (x)))+2(√2)∫_(π/2) ^π (dx/(2−cos^2 (x))) t=(π/2)+x in 2nd ⇒=2(√(2{))∫_0 ^(π/2) (dx/(1+sin^2 (x)))+∫_0 ^(π/2) (dx/(1+cos^2 ((x/2)))) =2(√2)∫_0 ^(π/2) (1/(sin^2 (x))).((dx/((1/(sin^2 (x)))+1)))+2(√2)∫_0 ^(π/2) (dx/(cos^2 (x))).(1/(((1/(cos^2 (x)))+1))) =2(√2)∫_0 ^(π/2) ((−d(cot(x)))/(2+cot^2 (x)))+2(√2)∫_0 ^(π/2) ((d(tg(x)))/(2+tg^2 (x))) =2([_0 ^(π/2) −arctan(((cot(x))/(√2)))+arctan(((tg(x))/(√2)))) =2.(π/2)+2.(π/2)=2π

$$=\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\sqrt{\mathrm{2}}−{cos}\left({x}\right)}+\int_{\pi} ^{\mathrm{2}\pi} \frac{{dx}}{\sqrt{\mathrm{2}}−{cos}\left({x}\right)} \\ $$$${t}=\pi+{x}\:{in}\:\mathrm{2}{nd}\Rightarrow \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\sqrt{\mathrm{2}}−{cos}\left({x}\right)}+\frac{{dx}}{\sqrt{\mathrm{2}}+{cos}\left({x}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}\sqrt{\mathrm{2}}{dx}}{\mathrm{2}−{cos}^{\mathrm{2}} \left({x}\right)}=\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{2}−{cos}^{\mathrm{2}} \left({x}\right)}+\mathrm{2}\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \frac{{dx}}{\mathrm{2}−{cos}^{\mathrm{2}} \left({x}\right)} \\ $$$${t}=\frac{\pi}{\mathrm{2}}+{x}\:{in}\:\mathrm{2}{nd} \\ $$$$\Rightarrow=\mathrm{2}\sqrt{\mathrm{2}\left\{\right.}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+{sin}^{\mathrm{2}} \left({x}\right)}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left({x}\right)}.\left(\frac{{dx}}{\frac{\mathrm{1}}{{sin}^{\mathrm{2}} \left({x}\right)}+\mathrm{1}}\right)+\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{cos}^{\mathrm{2}} \left({x}\right)}.\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)}+\mathrm{1}\right)} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{−{d}\left({cot}\left({x}\right)\right)}{\mathrm{2}+{cot}^{\mathrm{2}} \left({x}\right)}+\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tg}\left({x}\right)\right)}{\mathrm{2}+{tg}^{\mathrm{2}} \left({x}\right)} \\ $$$$=\mathrm{2}\left(\left[_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −{arctan}\left(\frac{{cot}\left({x}\right)}{\sqrt{\mathrm{2}}}\right)+{arctan}\left(\frac{{tg}\left({x}\right)}{\sqrt{\mathrm{2}}}\right)\right)\right. \\ $$$$=\mathrm{2}.\frac{\pi}{\mathrm{2}}+\mathrm{2}.\frac{\pi}{\mathrm{2}}=\mathrm{2}\pi \\ $$

Commented by jagoll last updated on 23/Mar/20

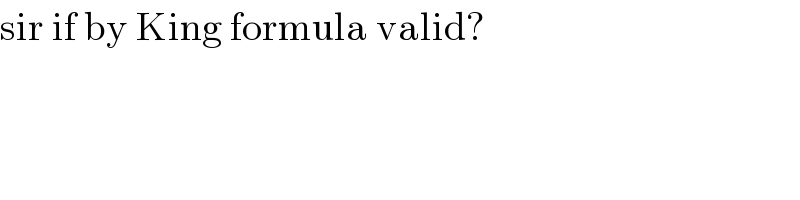
sir if by King formula valid?

$$\mathrm{sir}\:\mathrm{if}\:\mathrm{by}\:\mathrm{King}\:\mathrm{formula}\:\mathrm{valid}? \\ $$

Commented by mind is power last updated on 23/Mar/20

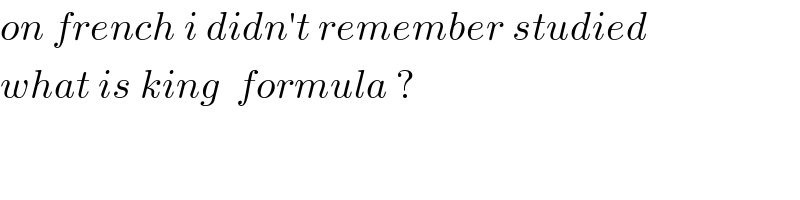
on french i didn′t remember studied what is king formula ?

$${on}\:{french}\:{i}\:{didn}'{t}\:{remember}\:{studied}\: \\ $$$${what}\:{is}\:{king}\:\:{formula}\:? \\ $$

Answered by mind is power last updated on 23/Mar/20

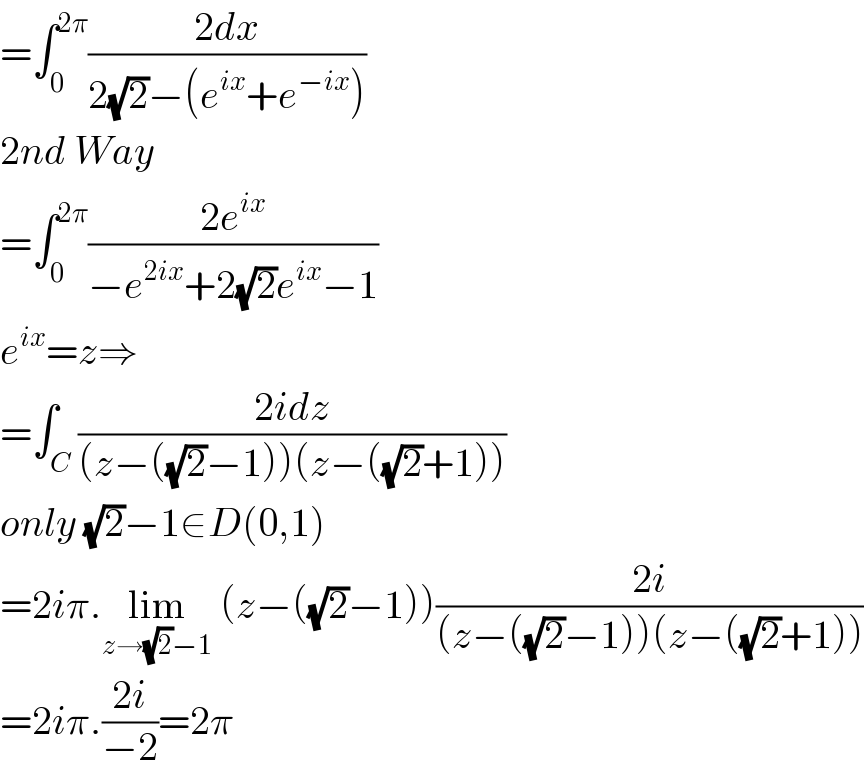
=∫_0 ^(2π) ((2dx)/(2(√2)−(e^(ix) +e^(−ix) ))) 2nd Way =∫_0 ^(2π) ((2e^(ix) )/(−e^(2ix) +2(√2)e^(ix) −1)) e^(ix) =z⇒ =∫_C ((2idz)/((z−((√2)−1))(z−((√2)+1)))) only (√2)−1∈D(0,1) =2iπ.lim_(z→(√2)−1) (z−((√2)−1))((2i)/((z−((√2)−1))(z−((√2)+1)))) =2iπ.((2i)/(−2))=2π

$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{2}{dx}}{\mathrm{2}\sqrt{\mathrm{2}}−\left({e}^{{ix}} +{e}^{−{ix}} \right)} \\ $$$$\mathrm{2}{nd}\:{Way} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{2}{e}^{{ix}} }{−{e}^{\mathrm{2}{ix}} +\mathrm{2}\sqrt{\mathrm{2}}{e}^{{ix}} −\mathrm{1}} \\ $$$${e}^{{ix}} ={z}\Rightarrow \\ $$$$=\int_{{C}} \frac{\mathrm{2}{idz}}{\left({z}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right)\left({z}−\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\right)} \\ $$$${only}\:\sqrt{\mathrm{2}}−\mathrm{1}\in{D}\left(\mathrm{0},\mathrm{1}\right) \\ $$$$=\mathrm{2}{i}\pi.\underset{{z}\rightarrow\sqrt{\mathrm{2}}−\mathrm{1}} {\mathrm{lim}}\:\left({z}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right)\frac{\mathrm{2}{i}}{\left({z}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right)\left({z}−\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\right)} \\ $$$$=\mathrm{2}{i}\pi.\frac{\mathrm{2}{i}}{−\mathrm{2}}=\mathrm{2}\pi \\ $$

Answered by mind is power last updated on 23/Mar/20

you can always dolve ∫((p(sin(t),cos(t)))/(Q(sin(t),cos(t))))dt withe P snd Q∈R[x][y] by tg((t/2))=x

$${you}\:{can}\:{always}\:\:{dolve}\:\int\frac{{p}\left({sin}\left({t}\right),{cos}\left({t}\right)\right)}{{Q}\left({sin}\left({t}\right),{cos}\left({t}\right)\right)}{dt} \\ $$$${withe}\:{P}\:{snd}\:{Q}\in\mathbb{R}\left[{x}\right]\left[{y}\right] \\ $$$${by}\:{tg}\left(\frac{{t}}{\mathrm{2}}\right)={x} \\ $$

Commented by jagoll last updated on 23/Mar/20

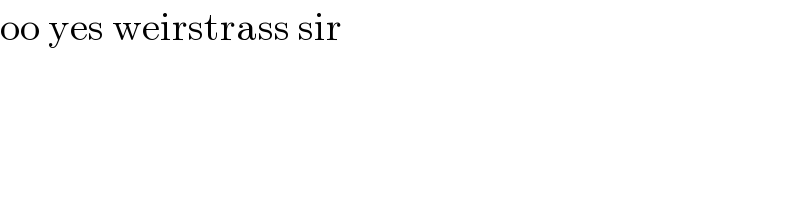
oo yes weirstrass sir

$$\mathrm{oo}\:\mathrm{yes}\:\mathrm{weirstrass}\:\mathrm{sir} \\ $$

Answered by MJS last updated on 23/Mar/20

∫(dx/((√2)−cos x))= [t=tan (x/2) →dx=(2/(t^2 +1))dt] =−2(1−(√2))∫(dt/(t^2 +3−2(√2)))= =2arctan ((1+(√2))t) = =2arctan ((1+(√2))tan (x/2)) +C

$$\int\frac{{dx}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow{dx}=\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\right] \\ $$$$=−\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}= \\ $$$$=\mathrm{2arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}\right)\:= \\ $$$$=\mathrm{2arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)\:+{C} \\ $$

Commented by jagoll last updated on 23/Mar/20

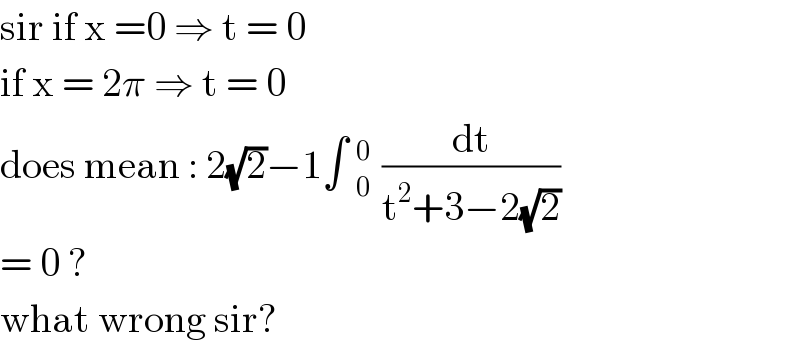
sir if x =0 ⇒ t = 0 if x = 2π ⇒ t = 0 does mean : 2(√2)−1∫ _(0 )^0 (dt/(t^2 +3−2(√2))) = 0 ? what wrong sir?

$$\mathrm{sir}\:\mathrm{if}\:\mathrm{x}\:=\mathrm{0}\:\Rightarrow\:\mathrm{t}\:=\:\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{x}\:=\:\mathrm{2}\pi\:\Rightarrow\:\mathrm{t}\:=\:\mathrm{0}\: \\ $$$$\mathrm{does}\:\mathrm{mean}\::\:\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\int\:_{\mathrm{0}\:} ^{\mathrm{0}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\:\mathrm{0}\:? \\ $$$$\mathrm{what}\:\mathrm{wrong}\:\mathrm{sir}? \\ $$

Commented by MJS last updated on 23/Mar/20

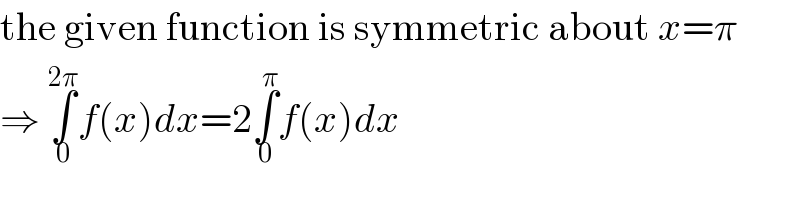
the given function is symmetric about x=π ⇒ ∫_0 ^(2π) f(x)dx=2∫_0 ^π f(x)dx

$$\mathrm{the}\:\mathrm{given}\:\mathrm{function}\:\mathrm{is}\:\mathrm{symmetric}\:\mathrm{about}\:{x}=\pi \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}{f}\left({x}\right){dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right){dx} \\ $$

Commented by MJS last updated on 23/Mar/20

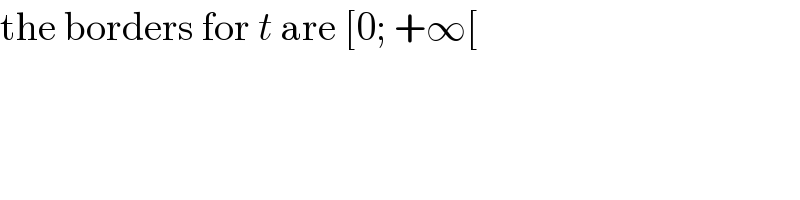
the borders for t are [0; +∞[

$$\mathrm{the}\:\mathrm{borders}\:\mathrm{for}\:{t}\:\mathrm{are}\:\left[\mathrm{0};\:+\infty\left[\right.\right. \\ $$

Commented by jagoll last updated on 23/Mar/20

2×2 [arc tan ((1+(√2))tan(x/2) )]_0 ^( (π/2)) 4 × [ arc tan ((1+(√2)) tan (π/4))] 4× [ arc tan ((1+(√2) ))] ?

$$\mathrm{2}×\mathrm{2}\:\left[\mathrm{arc}\:\mathrm{tan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}}\:\right)\underset{\mathrm{0}} {\overset{\:\frac{\pi}{\mathrm{2}}} {\right]}}\: \\ $$$$\mathrm{4}\:×\:\left[\:\mathrm{arc}\:\mathrm{tan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\mathrm{tan}\:\frac{\pi}{\mathrm{4}}\right)\right] \\ $$$$\mathrm{4}×\:\left[\:\mathrm{arc}\:\mathrm{tan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)\right)\right]\:?\: \\ $$$$ \\ $$$$ \\ $$

Commented by jagoll last updated on 23/Mar/20

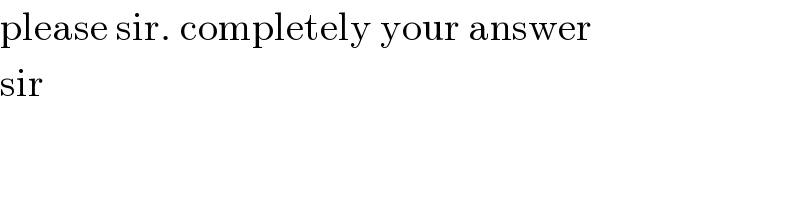
please sir. completely your answer sir

$$\mathrm{please}\:\mathrm{sir}.\:\mathrm{completely}\:\mathrm{your}\:\mathrm{answer} \\ $$$$\mathrm{sir} \\ $$

Commented by jagoll last updated on 23/Mar/20

or 4×[arc tan ((1+(√2))t]_( 0) ^∞ 4 ×[ arc tan (∞) − arc tan (0) ] 4×(π/2) = 2π

$$\mathrm{or}\:\mathrm{4}×\left[\mathrm{arc}\:\mathrm{tan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{t}\underset{\:\mathrm{0}} {\overset{\infty} {\right]}}\right. \\ $$$$\mathrm{4}\:×\left[\:\mathrm{arc}\:\mathrm{tan}\:\left(\infty\right)\:−\:\mathrm{arc}\:\mathrm{tan}\:\left(\mathrm{0}\right)\:\right] \\ $$$$\mathrm{4}×\frac{\pi}{\mathrm{2}}\:=\:\mathrm{2}\pi \\ $$

Commented by MJS last updated on 23/Mar/20

∫_0 ^(2π) (dx/((√2)−cos x))=2∫_0 ^π (dx/((√2)−cos x))= =2[2arctan ((1+(√2))tan (x/2))]_0 ^π = =4lim_(x→π^− ) (arctan ((1+(√2))tan (x/2))) =4×(π/2)=2π

$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\frac{{dx}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\:{x}}=\mathrm{2}\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\sqrt{\mathrm{2}}−\mathrm{cos}\:\:{x}}= \\ $$$$=\mathrm{2}\left[\mathrm{2arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\pi} = \\ $$$$=\mathrm{4}\underset{{x}\rightarrow\pi^{−} } {\mathrm{lim}}\:\left(\mathrm{arctan}\:\left(\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right)\right)\:=\mathrm{4}×\frac{\pi}{\mathrm{2}}=\mathrm{2}\pi \\ $$

Commented by jagoll last updated on 23/Mar/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com