
Question Number 216695 by sniper237 last updated on 16/Feb/25
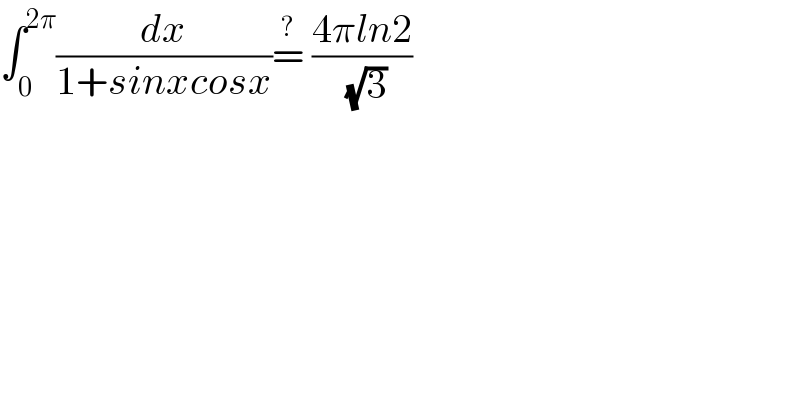
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\mathrm{1}+{sinxcosx}}\overset{?} {=}\:\frac{\mathrm{4}\pi{ln}\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\: \\ $$
Answered by Ghisom last updated on 16/Feb/25
![∫_0 ^(2π) (dx/(1+sin x cos x))=8∫_(π/4) ^(3π/4) (dx/(2+sin 2x))= =8∫_0 ^(π/2) (dx/(2+cos 2x))= [t=tan x] =8∫_0 ^∞ (dt/(t^2 +3))=((8(√3))/3)[arctan (((√3)t)/3)]_0 ^∞ = =((4π(√3))/3)](Q216709.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}=\mathrm{8}\underset{\pi/\mathrm{4}} {\overset{\mathrm{3}\pi/\mathrm{4}} {\int}}\frac{{dx}}{\mathrm{2}+\mathrm{sin}\:\mathrm{2}{x}}= \\ $$$$=\mathrm{8}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{dx}}{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\right] \\ $$$$=\mathrm{8}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}}=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{3}}\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$
