Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 143399 by Ar Brandon last updated on 13/Jun/21

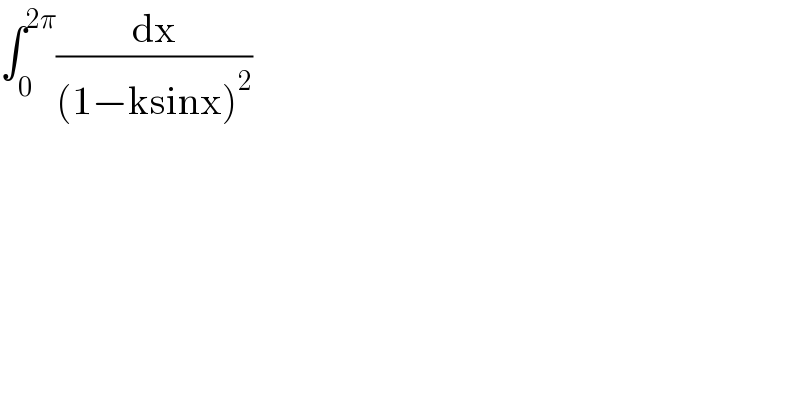
∫_0 ^(2π) (dx/((1−ksinx)^2 ))

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{ksinx}\right)^{\mathrm{2}} } \\ $$

Answered by Ar Brandon last updated on 13/Jun/21

I=∫_0 ^(2π) (dx/((1−ksinx)^2 ))=2∫_(−(π/2)) ^(π/2) (dx/((1−ksinx)^2 )) t=tan(x/2) =2∫_(−1) ^1 (1/((1−k((2t)/(1+t^2 )))^2 ))∙((2dt)/(1+t^2 ))=4∫_(−1) ^1 ((t^2 +1)/((t^2 −2kt+1)^2 ))dt =4[((at+b)/(t^2 −2kt+1))+∫((ct+d)/(t^2 −2kt+1))dt]_(−1) ^1 =4∫[((a(t^2 −2kt+1)−(at+b)(2t−2k))/((t^2 +2kt+1)^2 ))+((ct+d)/(t^2 −2kt+1))]dt c=0,a−2a+d=1⇒d=a+1,−2ka+2ka−2b−2kd=0⇒b=−kd a+2bk+d=1⇒d+bk=1⇒d(1−k^2 )=1⇒d=(1/(1−k^2 )),b=(k/(k^2 −1)) ⇒a=(1/(1−k^2 ))−1=((1+k^2 −1)/(1−k^2 ))=(k^2 /(1−k^2 )) I=4[(((k^2 /(1−k^2 ))t+(k/(k^2 −1)))/(t^2 −2kt+1))+(1/(1−k^2 ))∫(dt/(t^2 −2kt+1))]_(−1) ^1 =(4/(2−2k))((k^2 /(1−k^2 ))+(1/(k^2 −1)))−(4/(2+2k))((k/(k^2 −1))−(k^2 /(1−k^2 )))+(4/(1−k^2 ))∫(dt/(t^2 −2kt+1)) ∫(dt/(t^2 −2kt+1))=∫(dt/((t−k)^2 +1−k^2 ))=(1/( (√(1−k^2 ))))arctan(((t−k)/( (√(1−k^2 ))))), ∣k∣<1 ∫(dt/(t^2 −2kt+1))=∫(dt/((t−k)^2 −(k^2 −1)))=((−1)/( (√(k^2 −1))))argtanh(((t−k)/( (√(k^2 −1))))), ∣k∣>1 I=(2/(k−1))−(2/(k+1))((k/(k−1)))+((4(√(1−k^2 )))/( (1−k^2 )^2 ))[arctan((√((1−k)/(1+k))))+arctan(((k+1)/( (√(1−k^2 )))))], ∣k∣<1 =(2/(k−1))−(2/(k+1))((k/(k−1)))+((2(√(k^2 −1)))/((k^2 −1)^2 ))ln∣(((√(k^2 −1))−k+1)/( (√(k^2 −1))+k−1))∣, ∣k∣>1

$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{ksinx}\right)^{\mathrm{2}} }=\mathrm{2}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{ksinx}\right)^{\mathrm{2}} }\:\mathrm{t}=\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\:\:=\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{k}\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\mathrm{4}\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:=\mathrm{4}\left[\frac{\mathrm{at}+\mathrm{b}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}+\int\frac{\mathrm{ct}+\mathrm{d}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}\mathrm{dt}\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$\:\:=\mathrm{4}\int\left[\frac{\mathrm{a}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}\right)−\left(\mathrm{at}+\mathrm{b}\right)\left(\mathrm{2t}−\mathrm{2k}\right)}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2kt}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{ct}+\mathrm{d}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}\right]\mathrm{dt} \\ $$$$\mathrm{c}=\mathrm{0},\mathrm{a}−\mathrm{2a}+\mathrm{d}=\mathrm{1}\Rightarrow\mathrm{d}=\mathrm{a}+\mathrm{1},−\mathrm{2ka}+\mathrm{2ka}−\mathrm{2b}−\mathrm{2kd}=\mathrm{0}\Rightarrow\mathrm{b}=−\mathrm{kd} \\ $$$$\mathrm{a}+\mathrm{2bk}+\mathrm{d}=\mathrm{1}\Rightarrow\mathrm{d}+\mathrm{bk}=\mathrm{1}\Rightarrow\mathrm{d}\left(\mathrm{1}−\mathrm{k}^{\mathrm{2}} \right)=\mathrm{1}\Rightarrow\mathrm{d}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{k}^{\mathrm{2}} },\mathrm{b}=\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow\mathrm{a}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }−\mathrm{1}=\frac{\mathrm{1}+\mathrm{k}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }=\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{1}−\mathrm{k}^{\mathrm{2}} } \\ $$$$\mathrm{I}=\mathrm{4}\left[\frac{\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }\mathrm{t}+\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$\:\:=\frac{\mathrm{4}}{\mathrm{2}−\mathrm{2k}}\left(\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}\right)−\frac{\mathrm{4}}{\mathrm{2}+\mathrm{2k}}\left(\frac{\mathrm{k}}{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }\right)+\frac{\mathrm{4}}{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}} \\ $$$$\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}=\int\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{k}\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }}\mathrm{arctan}\left(\frac{\mathrm{t}−\mathrm{k}}{\:\sqrt{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }}\right),\:\mid\mathrm{k}\mid<\mathrm{1} \\ $$$$\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2kt}+\mathrm{1}}=\int\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{k}\right)^{\mathrm{2}} −\left(\mathrm{k}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}\mathrm{argtanh}\left(\frac{\mathrm{t}−\mathrm{k}}{\:\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}\right),\:\mid\mathrm{k}\mid>\mathrm{1} \\ $$$$\mathrm{I}=\frac{\mathrm{2}}{\mathrm{k}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{k}+\mathrm{1}}\left(\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}\right)+\frac{\mathrm{4}\sqrt{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }}{\:\left(\mathrm{1}−\mathrm{k}^{\mathrm{2}} \right)^{\mathrm{2}} }\left[\mathrm{arctan}\left(\sqrt{\frac{\mathrm{1}−\mathrm{k}}{\mathrm{1}+\mathrm{k}}}\right)+\mathrm{arctan}\left(\frac{\mathrm{k}+\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{k}^{\mathrm{2}} }}\right)\right],\:\mid\mathrm{k}\mid<\mathrm{1} \\ $$$$\:\:=\frac{\mathrm{2}}{\mathrm{k}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{k}+\mathrm{1}}\left(\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}\right)+\frac{\mathrm{2}\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}{\left(\mathrm{k}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{ln}\mid\frac{\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}−\mathrm{k}+\mathrm{1}}{\:\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}+\mathrm{k}−\mathrm{1}}\mid,\:\mid\mathrm{k}\mid>\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 13/Jun/21

Please check !

$$\mathrm{Please}\:\mathrm{check}\:! \\ $$

Answered by mathmax by abdo last updated on 13/Jun/21

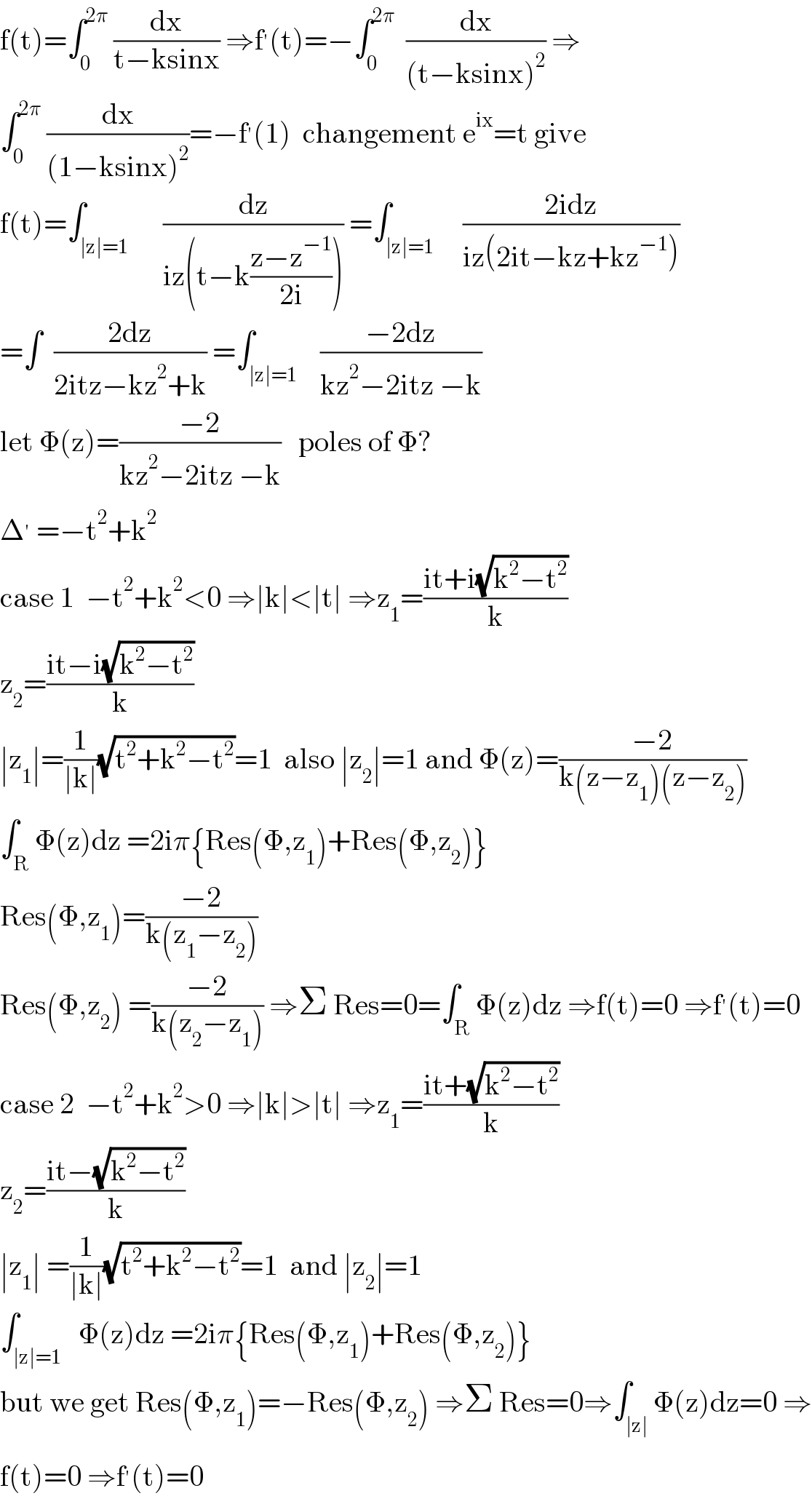
f(t)=∫_0 ^(2π) (dx/(t−ksinx)) ⇒f^′ (t)=−∫_0 ^(2π) (dx/((t−ksinx)^2 )) ⇒ ∫_0 ^(2π) (dx/((1−ksinx)^2 ))=−f^′ (1) changement e^(ix) =t give f(t)=∫_(∣z∣=1) (dz/(iz(t−k((z−z^(−1) )/(2i))))) =∫_(∣z∣=1) ((2idz)/(iz(2it−kz+kz^(−1) ))) =∫ ((2dz)/(2itz−kz^2 +k)) =∫_(∣z∣=1) ((−2dz)/(kz^2 −2itz −k)) let Φ(z)=((−2)/(kz^2 −2itz −k)) poles of Φ? Δ^′ =−t^2 +k^2 case 1 −t^2 +k^2 <0 ⇒∣k∣<∣t∣ ⇒z_1 =((it+i(√(k^2 −t^2 )))/k) z_2 =((it−i(√(k^2 −t^2 )))/k) ∣z_1 ∣=(1/(∣k∣))(√(t^2 +k^2 −t^2 ))=1 also ∣z_2 ∣=1 and Φ(z)=((−2)/(k(z−z_1 )(z−z_2 ))) ∫_R Φ(z)dz =2iπ{Res(Φ,z_1 )+Res(Φ,z_2 )} Res(Φ,z_1 )=((−2)/(k(z_1 −z_2 ))) Res(Φ,z_2 ) =((−2)/(k(z_2 −z_1 ))) ⇒Σ Res=0=∫_R Φ(z)dz ⇒f(t)=0 ⇒f^′ (t)=0 case 2 −t^2 +k^2 >0 ⇒∣k∣>∣t∣ ⇒z_1 =((it+(√(k^2 −t^2 )))/k) z_2 =((it−(√(k^2 −t^2 )))/k) ∣z_1 ∣ =(1/(∣k∣))(√(t^2 +k^2 −t^2 ))=1 and ∣z_2 ∣=1 ∫_(∣z∣=1) Φ(z)dz =2iπ{Res(Φ,z_1 )+Res(Φ,z_2 )} but we get Res(Φ,z_1 )=−Res(Φ,z_2 ) ⇒Σ Res=0⇒∫_(∣z∣) Φ(z)dz=0 ⇒ f(t)=0 ⇒f^′ (t)=0

$$\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{t}−\mathrm{ksinx}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)=−\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{dx}}{\left(\mathrm{t}−\mathrm{ksinx}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{1}−\mathrm{ksinx}\right)^{\mathrm{2}} }=−\mathrm{f}^{'} \left(\mathrm{1}\right)\:\:\mathrm{changement}\:\mathrm{e}^{\mathrm{ix}} =\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{t}−\mathrm{k}\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2i}}\right)}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2idz}}{\mathrm{iz}\left(\mathrm{2it}−\mathrm{kz}+\mathrm{kz}^{−\mathrm{1}} \right)} \\ $$$$=\int\:\:\frac{\mathrm{2dz}}{\mathrm{2itz}−\mathrm{kz}^{\mathrm{2}} +\mathrm{k}}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2dz}}{\mathrm{kz}^{\mathrm{2}} −\mathrm{2itz}\:−\mathrm{k}} \\ $$$$\mathrm{let}\:\Phi\left(\mathrm{z}\right)=\frac{−\mathrm{2}}{\mathrm{kz}^{\mathrm{2}} −\mathrm{2itz}\:−\mathrm{k}}\:\:\:\mathrm{poles}\:\mathrm{of}\:\Phi? \\ $$$$\Delta^{'} \:=−\mathrm{t}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \\ $$$$\mathrm{case}\:\mathrm{1}\:\:−\mathrm{t}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\mid\mathrm{k}\mid<\mid\mathrm{t}\mid\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{it}+\mathrm{i}\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} }}{\mathrm{k}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{it}−\mathrm{i}\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} }}{\mathrm{k}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid=\frac{\mathrm{1}}{\mid\mathrm{k}\mid}\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} }=\mathrm{1}\:\:\mathrm{also}\:\mid\mathrm{z}_{\mathrm{2}} \mid=\mathrm{1}\:\mathrm{and}\:\Phi\left(\mathrm{z}\right)=\frac{−\mathrm{2}}{\mathrm{k}\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\int_{\mathrm{R}} \Phi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{1}} \right)+\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{2}} \right)\right\} \\ $$$$\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{1}} \right)=\frac{−\mathrm{2}}{\mathrm{k}\left(\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{2}} \right)\:=\frac{−\mathrm{2}}{\mathrm{k}\left(\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} \right)}\:\Rightarrow\Sigma\:\mathrm{Res}=\mathrm{0}=\int_{\mathrm{R}} \Phi\left(\mathrm{z}\right)\mathrm{dz}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)=\mathrm{0} \\ $$$$\mathrm{case}\:\mathrm{2}\:\:−\mathrm{t}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\mid\mathrm{k}\mid>\mid\mathrm{t}\mid\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{it}+\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} }}{\mathrm{k}} \\ $$$$\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{it}−\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} }}{\mathrm{k}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid\:=\frac{\mathrm{1}}{\mid\mathrm{k}\mid}\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} }=\mathrm{1}\:\:\mathrm{and}\:\mid\mathrm{z}_{\mathrm{2}} \mid=\mathrm{1} \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\Phi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{1}} \right)+\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{2}} \right)\right\} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{get}\:\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{1}} \right)=−\mathrm{Res}\left(\Phi,\mathrm{z}_{\mathrm{2}} \right)\:\Rightarrow\Sigma\:\mathrm{Res}=\mathrm{0}\Rightarrow\int_{\mid\mathrm{z}\mid} \Phi\left(\mathrm{z}\right)\mathrm{dz}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{t}\right)=\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)=\mathrm{0} \\ $$

Commented by Ar Brandon last updated on 13/Jun/21

Hum... The^� ore^� me de Re^� sidus. Thanks Sir ! Grateful !

$$\mathrm{Hum}...\:\mathrm{Th}\acute {\mathrm{e}or}\grave {\mathrm{e}me}\:\mathrm{de}\:\mathrm{R}\acute {\mathrm{e}sidus}. \\ $$$$\mathrm{Thanks}\:\mathrm{Sir}\:!\:\mathrm{Grateful}\:! \\ $$

Commented by mathmax by abdo last updated on 13/Jun/21

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com