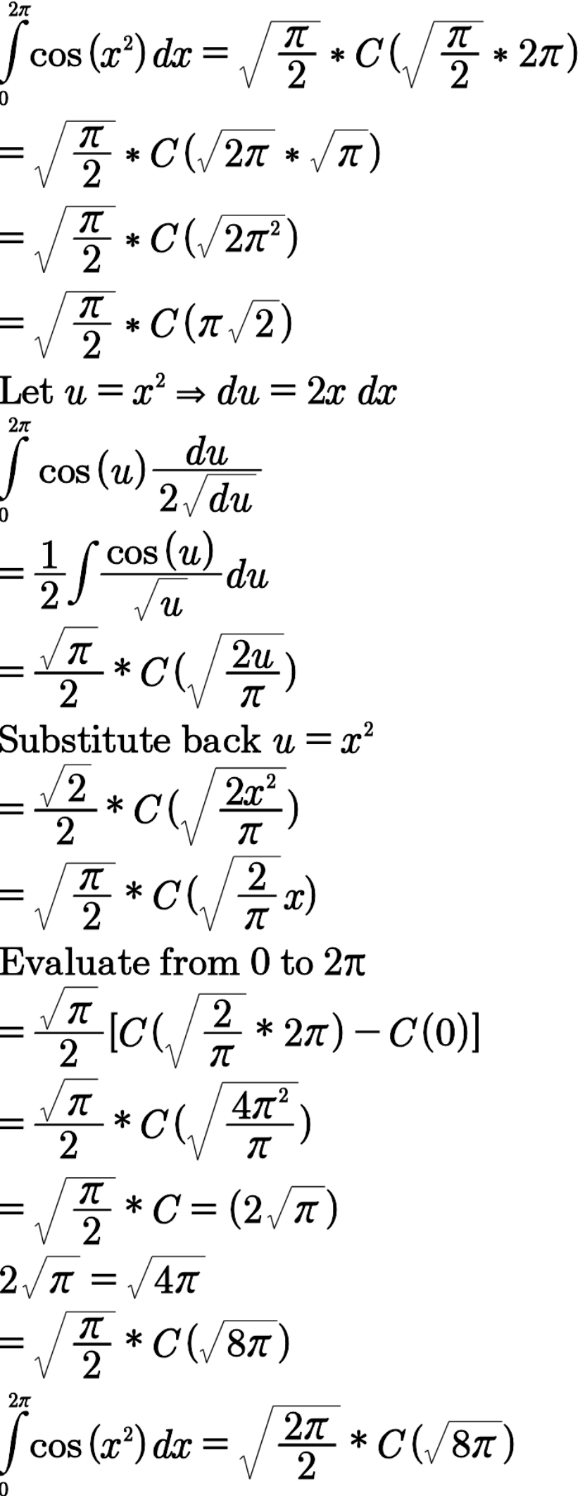Question Number 218063 by alephnull last updated on 27/Mar/25

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\mathrm{cos}\:{x}^{\mathrm{2}} \\ $$
Answered by Frix last updated on 28/Mar/25
![The Fresnel C Integral: C (x) := ∫_0 ^x cos ((πt^2 )/2) dt ⇒ ∫_0 ^(2π) cos x^2 dx=((√(2π))/2)[C (((√2)/( (√π)))x)]_0 ^(2π) =((√(2π))/2)C ((√(8π))) ≈.704681810](Q218064.png)
$$\mathrm{The}\:\mathrm{Fresnel}\:\mathrm{C}\:\mathrm{Integral}: \\ $$$$\mathrm{C}\:\left({x}\right)\::=\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\mathrm{cos}\:\frac{\pi{t}^{\mathrm{2}} }{\mathrm{2}}\:{dt} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\mathrm{cos}\:{x}^{\mathrm{2}} \:{dx}=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{2}}\left[\mathrm{C}\:\left(\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\pi}}{x}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} =\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{2}}\mathrm{C}\:\left(\sqrt{\mathrm{8}\pi}\right) \\ $$$$\approx.\mathrm{704681810} \\ $$
Answered by MrGaster last updated on 29/Mar/25