Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 10495 by ajfour last updated on 14/Feb/17

∫_0 ^(2π) (√(R^2 +r^2 −2Rrcos θ)) dθ

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rr}\mathrm{cos}\:\theta}\:{d}\theta \\ $$

Answered by robocop last updated on 14/Feb/17

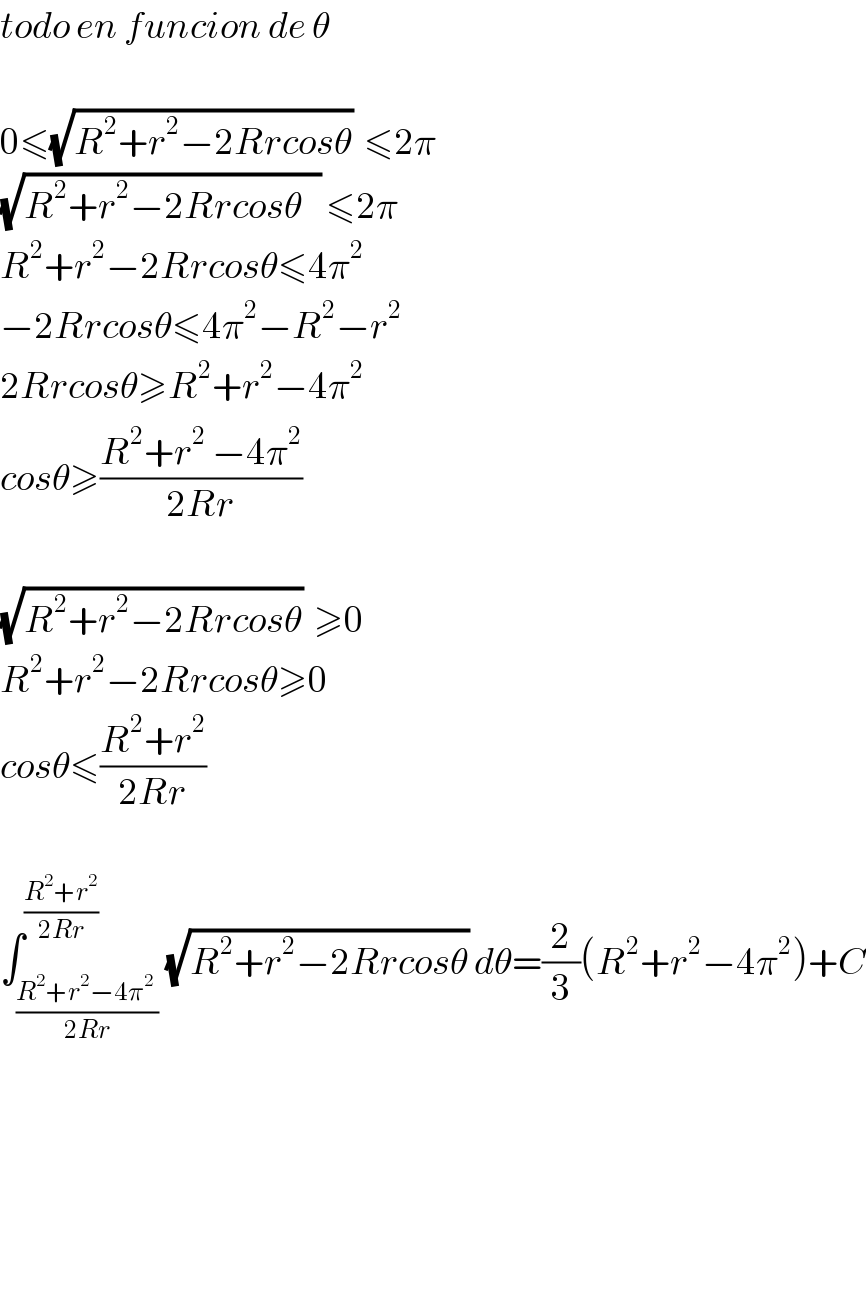
todo en funcion de θ 0≤(√(R^2 +r^2 −2Rrcosθ)) ≤2π (√(R^2 +r^2 −2Rrcosθ )) ≤2π R^2 +r^2 −2Rrcosθ≤4π^2 −2Rrcosθ≤4π^2 −R^2 −r^2 2Rrcosθ≥R^2 +r^2 −4π^2 cosθ≥((R^2 +r^2^ −4π^2 )/(2Rr)) (√(R^2 +r^2 −2Rrcosθ)) ≥0 R^2 +r^2 −2Rrcosθ≥0 cosθ≤((R^2 +r^2 )/(2Rr)) ∫_((R^2 +r^2 −4π^(2 ) )/(2Rr)) ^((R^2 +r^2 )/(2Rr)) (√(R^2 +r^2 −2Rrcosθ)) dθ=(2/3)(R^2 +r^2 −4π^2 )+C

$${todo}\:{en}\:{funcion}\:{de}\:\theta \\ $$$$ \\ $$$$\mathrm{0}\leqslant\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rrcos}\theta}\:\:\leqslant\mathrm{2}\pi \\ $$$$\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rrcos}\theta\:\:\:}\:\leqslant\mathrm{2}\pi \\ $$$${R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rrcos}\theta\leqslant\mathrm{4}\pi^{\mathrm{2}} \\ $$$$−\mathrm{2}{Rrcos}\theta\leqslant\mathrm{4}\pi^{\mathrm{2}} −{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$$\mathrm{2}{Rrcos}\theta\geqslant{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{4}\pi^{\mathrm{2}} \\ $$$${cos}\theta\geqslant\frac{{R}^{\mathrm{2}} +{r}^{\mathrm{2}^{} } −\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{2}{Rr}} \\ $$$$ \\ $$$$\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rrcos}\theta}\:\:\geqslant\mathrm{0} \\ $$$${R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rrcos}\theta\geqslant\mathrm{0} \\ $$$${cos}\theta\leqslant\frac{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{2}{Rr}} \\ $$$$ \\ $$$$\int_{\frac{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{4}\pi^{\mathrm{2}\:\:} }{\mathrm{2}{Rr}}} ^{\frac{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{2}{Rr}}} \sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rrcos}\theta}\:{d}\theta=\frac{\mathrm{2}}{\mathrm{3}}\left({R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{4}\pi^{\mathrm{2}} \right)+{C} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by ajfour last updated on 16/Feb/17

not satisfied.

$${not}\:{satisfied}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com