
Question Number 42410 by soufiane zarik last updated on 25/Aug/18
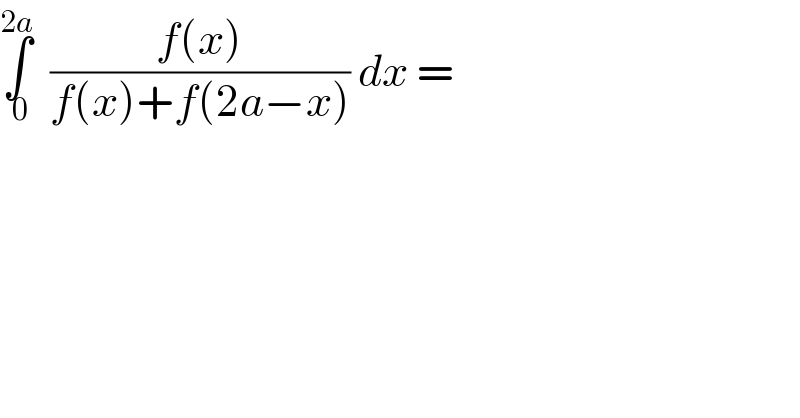
$$\underset{\:\mathrm{0}} {\overset{\mathrm{2}{a}} {\int}}\:\:\frac{{f}\left({x}\right)}{{f}\left({x}\right)+{f}\left(\mathrm{2}{a}−{x}\right)}\:{dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 25/Aug/18
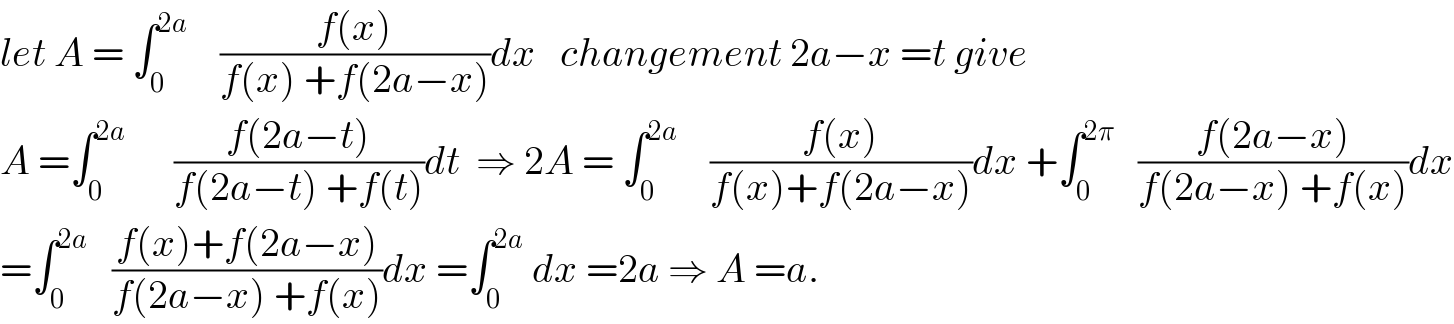
$${let}\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}{a}} \:\:\:\:\frac{{f}\left({x}\right)}{{f}\left({x}\right)\:+{f}\left(\mathrm{2}{a}−{x}\right)}{dx}\:\:\:{changement}\:\mathrm{2}{a}−{x}\:={t}\:{give} \\ $$$${A}\:=\int_{\mathrm{0}} ^{\mathrm{2}{a}} \:\:\:\:\:\:\frac{{f}\left(\mathrm{2}{a}−{t}\right)}{{f}\left(\mathrm{2}{a}−{t}\right)\:+{f}\left({t}\right)}{dt}\:\:\Rightarrow\:\mathrm{2}{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}{a}} \:\:\:\:\frac{{f}\left({x}\right)}{{f}\left({x}\right)+{f}\left(\mathrm{2}{a}−{x}\right)}{dx}\:+\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{f}\left(\mathrm{2}{a}−{x}\right)}{{f}\left(\mathrm{2}{a}−{x}\right)\:+{f}\left({x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}{a}} \:\:\:\frac{{f}\left({x}\right)+{f}\left(\mathrm{2}{a}−{x}\right)}{{f}\left(\mathrm{2}{a}−{x}\right)\:+{f}\left({x}\right)}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{2}{a}} \:{dx}\:=\mathrm{2}{a}\:\Rightarrow\:{A}\:={a}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Aug/18
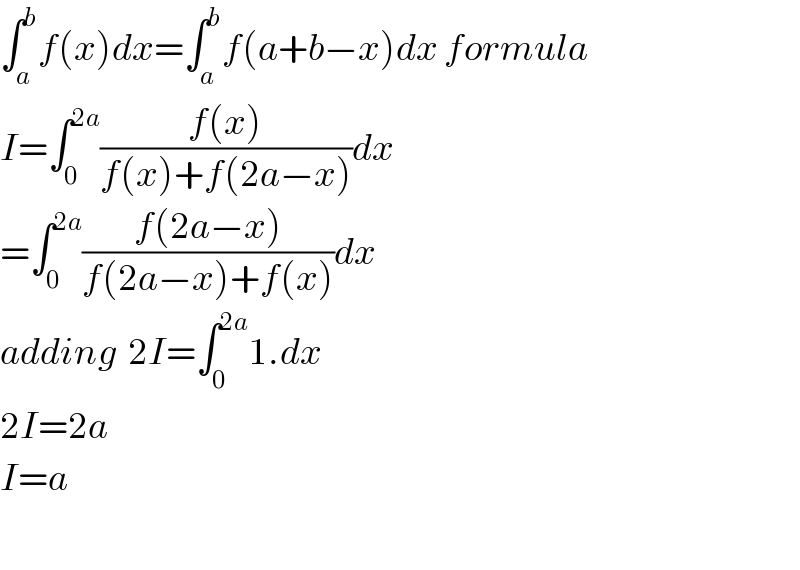
$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx}\:{formula} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{2}{a}} \frac{{f}\left({x}\right)}{{f}\left({x}\right)+{f}\left(\mathrm{2}{a}−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}{a}} \frac{{f}\left(\mathrm{2}{a}−{x}\right)}{{f}\left(\mathrm{2}{a}−{x}\right)+{f}\left({x}\right)}{dx} \\ $$$${adding}\:\:\mathrm{2}{I}=\int_{\mathrm{0}} ^{\mathrm{2}{a}} \mathrm{1}.{dx} \\ $$$$\mathrm{2}{I}=\mathrm{2}{a} \\ $$$${I}={a} \\ $$$$ \\ $$
