
Question Number 67197 by necxxx last updated on 23/Aug/19
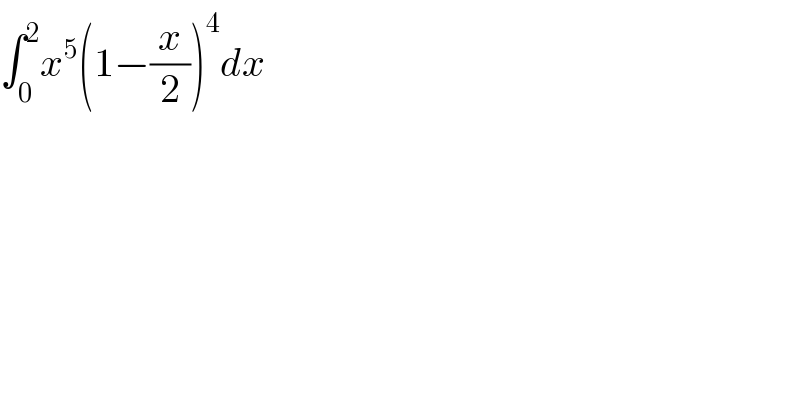
$$\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\mathrm{5}} \left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{4}} {dx} \\ $$
Answered by turbo msup by abdo last updated on 24/Aug/19
![I =(1/(16)) ∫_0 ^2 x^5 (x−2)^4 dx =(1/(16)) ∫_0 ^2 x^5 Σ_(k=0) ^4 C_4 ^k x^k (−2)^(4−k) 16I=Σ_(k=0) ^4 C_4 ^k (−2)^(4−k) ∫_0 ^2 x^(k+5) dx =16 Σ_(k=0) ^4 C_4 ^k (−2)^(−k) [(1/(k+6))x^(k+6) ]_0 ^2 ⇒I =Σ_(k=0) ^4 (−2)^(−k) C_4 ^k ×(2^(k+6) /(k+6))](Q67199.png)
$${I}\:=\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\mathrm{5}} \left({x}−\mathrm{2}\right)^{\mathrm{4}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\mathrm{5}} \sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} {x}^{{k}} \left(−\mathrm{2}\right)^{\mathrm{4}−{k}} \\ $$$$\mathrm{16}{I}=\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \left(−\mathrm{2}\right)^{\mathrm{4}−{k}} \int_{\mathrm{0}} ^{\mathrm{2}} \:{x}^{{k}+\mathrm{5}} \:{dx} \\ $$$$=\mathrm{16}\:\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:\left(−\mathrm{2}\right)^{−{k}} \:\left[\frac{\mathrm{1}}{{k}+\mathrm{6}}{x}^{{k}+\mathrm{6}} \right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\Rightarrow{I}\:=\overset{\mathrm{4}} {\sum}_{{k}=\mathrm{0}} \left(−\mathrm{2}\right)^{−{k}} \:{C}_{\mathrm{4}} ^{{k}} \:×\frac{\mathrm{2}^{{k}+\mathrm{6}} }{{k}+\mathrm{6}} \\ $$
