
Question Number 85717 by M±th+et£s last updated on 24/Mar/20
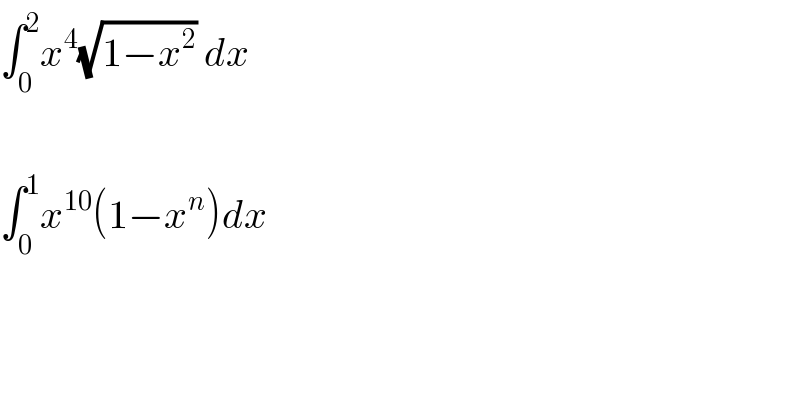
$$\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\mathrm{4}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{10}} \left(\mathrm{1}−{x}^{{n}} \right){dx} \\ $$$$ \\ $$
Answered by mind is power last updated on 24/Mar/20
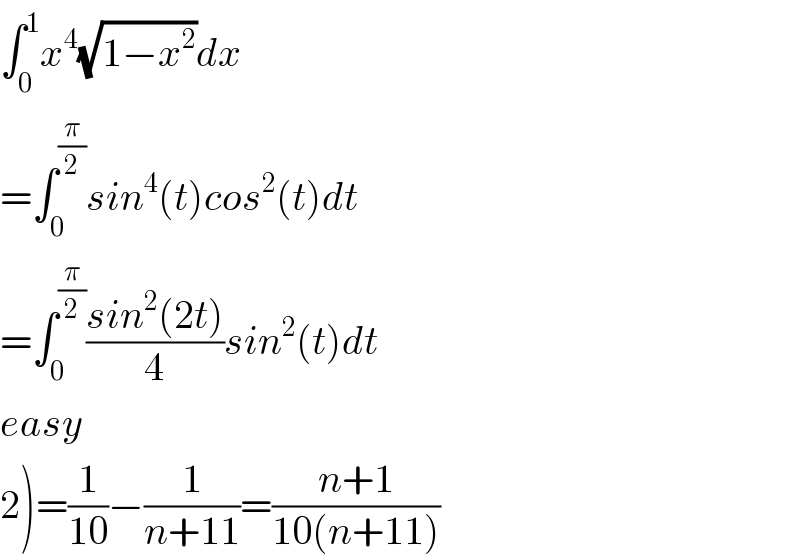
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{4}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{4}} \left({t}\right){cos}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} \left(\mathrm{2}{t}\right)}{\mathrm{4}}{sin}^{\mathrm{2}} \left({t}\right){dt} \\ $$$${easy} \\ $$$$\left.\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{{n}+\mathrm{11}}=\frac{{n}+\mathrm{1}}{\mathrm{10}\left({n}+\mathrm{11}\right)} \\ $$
Commented by M±th+et£s last updated on 24/Mar/20

$${thank}\:{you}\:{sir} \\ $$
