
Question Number 24825 by A1B1C1D1 last updated on 27/Nov/17
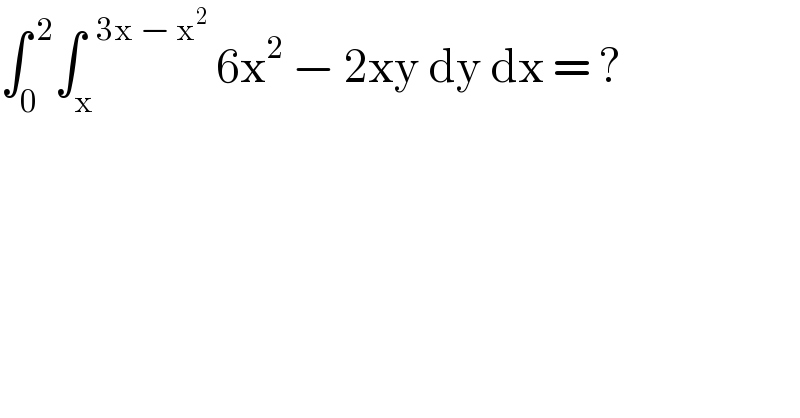
$$\int_{\mathrm{0}} ^{\:\mathrm{2}} \int_{\mathrm{x}} ^{\:\:\mathrm{3x}\:−\:\mathrm{x}^{\mathrm{2}} } \:\mathrm{6x}^{\mathrm{2}} \:−\:\mathrm{2xy}\:\mathrm{dy}\:\mathrm{dx}\:=\:? \\ $$
Commented by 1kanika# last updated on 27/Nov/17

$$\mathrm{32}. \\ $$
Commented by A1B1C1D1 last updated on 27/Nov/17

$$\mathrm{Thank}\:\mathrm{you}. \\ $$
Commented by maxmathsup by imad last updated on 24/May/19
![I =∫_0 ^2 A(x)dx with A(x) =∫_x ^(3x−x^2 ) (6x^2 −2xy)dy ⇒ A(x) =6x^2 (3x−x^2 −x) −2x ∫_x ^(3x−x^2 ) ydy =12x^3 −6x^4 −x[y^2 ]_x ^(3x−x^2 ) =12x^3 −6x^4 −x( (3x−x^2 )^2 −x^2 ) =12x^3 −6x^4 −x( 9x^2 −6x^3 +x^4 −x^2 ) =12x^3 −6x^4 −8x^3 +6x^4 −x^5 =4x^3 −x^5 ⇒ I =∫_0 ^2 (4x^3 −x^5 )dx =[x^4 −(1/6)x^6 ]_0 ^2 =2^4 −(2^6 /6) =16−((16.4)/6) =16 −((16.2)/3) =((48−32)/3) =((16)/3) .](Q60711.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:{A}\left({x}\right){dx}\:\:{with}\:{A}\left({x}\right)\:=\int_{{x}} ^{\mathrm{3}{x}−{x}^{\mathrm{2}} } \left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}{xy}\right){dy}\:\Rightarrow \\ $$$${A}\left({x}\right)\:=\mathrm{6}{x}^{\mathrm{2}} \left(\mathrm{3}{x}−{x}^{\mathrm{2}} −{x}\right)\:−\mathrm{2}{x}\:\int_{{x}} ^{\mathrm{3}{x}−{x}^{\mathrm{2}} } {ydy} \\ $$$$=\mathrm{12}{x}^{\mathrm{3}} \:−\mathrm{6}{x}^{\mathrm{4}} \:−{x}\left[{y}^{\mathrm{2}} \right]_{{x}} ^{\mathrm{3}{x}−{x}^{\mathrm{2}} } \:=\mathrm{12}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{4}} \:−{x}\left(\:\:\left(\mathrm{3}{x}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} −{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{12}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{4}} \:−{x}\left(\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{6}{x}^{\mathrm{3}} \:+{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{12}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{4}} \:−{x}^{\mathrm{5}} \:=\mathrm{4}{x}^{\mathrm{3}} \:−{x}^{\mathrm{5}} \:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\left(\mathrm{4}{x}^{\mathrm{3}} −{x}^{\mathrm{5}} \right){dx} \\ $$$$=\left[{x}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{6}} \right]_{\mathrm{0}} ^{\mathrm{2}} \:=\mathrm{2}^{\mathrm{4}} −\frac{\mathrm{2}^{\mathrm{6}} }{\mathrm{6}}\:=\mathrm{16}−\frac{\mathrm{16}.\mathrm{4}}{\mathrm{6}}\:=\mathrm{16}\:−\frac{\mathrm{16}.\mathrm{2}}{\mathrm{3}}\:=\frac{\mathrm{48}−\mathrm{32}}{\mathrm{3}}\:=\frac{\mathrm{16}}{\mathrm{3}}\:. \\ $$
Answered by ajfour last updated on 27/Nov/17
![∫_0 ^( 2) [6x^2 y−xy^2 ]∣_x ^(3x−x^2 ) dx =∫_0 ^( 2) 6x^2 (2x−x^2 )dx−∫_0 ^( 2) x[(x^4 −6x^3 +8x^2 ]dx =[3x^4 −(6/5)x^5 −(x^6 /6)+(6/5)x^5 −2x^4 ]∣_0 ^2 =16−((32)/3)= ((16)/3) .](Q24844.png)
$$\int_{\mathrm{0}} ^{\:\:\mathrm{2}} \left[\mathrm{6}{x}^{\mathrm{2}} {y}−{xy}^{\mathrm{2}} \right]\mid_{{x}} ^{\mathrm{3}{x}−{x}^{\mathrm{2}} } {dx} \\ $$$$=\int_{\mathrm{0}} ^{\:\:\mathrm{2}} \mathrm{6}{x}^{\mathrm{2}} \left(\mathrm{2}{x}−{x}^{\mathrm{2}} \right){dx}−\int_{\mathrm{0}} ^{\:\:\mathrm{2}} {x}\left[\left({x}^{\mathrm{4}} −\mathrm{6}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} \right]{dx}\right. \\ $$$$=\left[\mathrm{3}{x}^{\mathrm{4}} −\frac{\mathrm{6}}{\mathrm{5}}{x}^{\mathrm{5}} −\frac{{x}^{\mathrm{6}} }{\mathrm{6}}+\frac{\mathrm{6}}{\mathrm{5}}{x}^{\mathrm{5}} −\mathrm{2}{x}^{\mathrm{4}} \right]\mid_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{16}−\frac{\mathrm{32}}{\mathrm{3}}=\:\frac{\mathrm{16}}{\mathrm{3}}\:. \\ $$
