
Question Number 7300 by Tawakalitu. last updated on 22/Aug/16
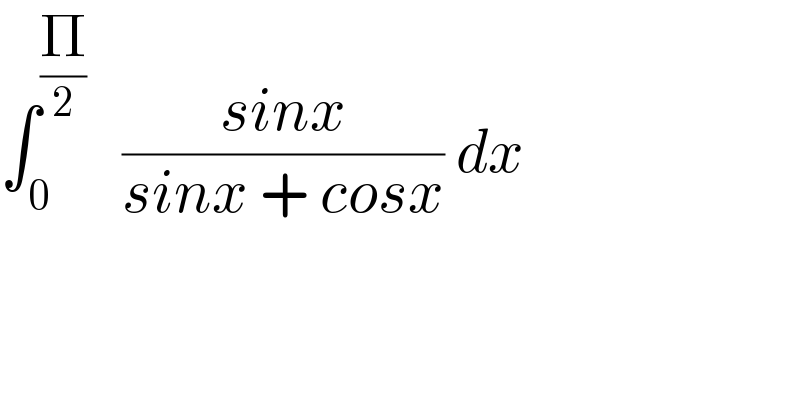
$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \:\:\:\frac{{sinx}}{{sinx}\:+\:{cosx}}\:{dx}\: \\ $$
Answered by Yozzia last updated on 22/Aug/16
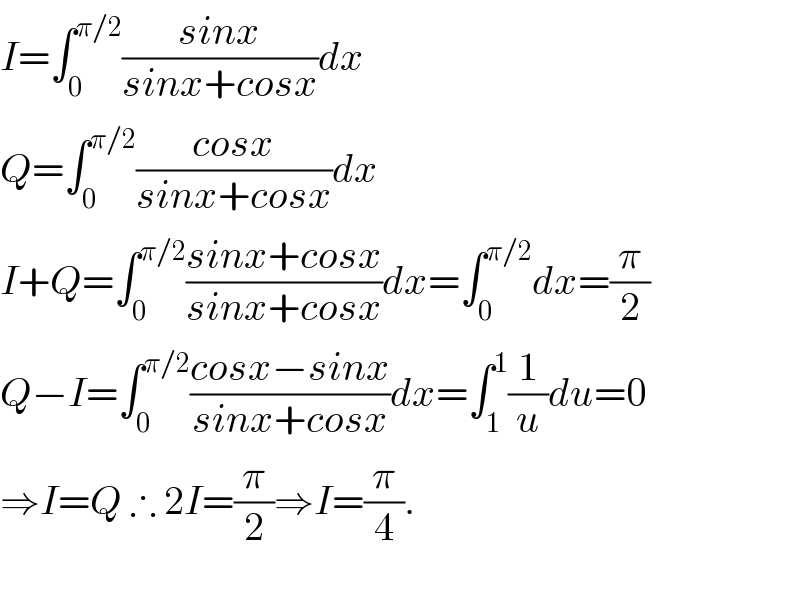
$${I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sinx}}{{sinx}+{cosx}}{dx} \\ $$$${Q}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{cosx}}{{sinx}+{cosx}}{dx} \\ $$$${I}+{Q}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sinx}+{cosx}}{{sinx}+{cosx}}{dx}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {dx}=\frac{\pi}{\mathrm{2}} \\ $$$${Q}−{I}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{cosx}−{sinx}}{{sinx}+{cosx}}{dx}=\int_{\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{1}}{{u}}{du}=\mathrm{0} \\ $$$$\Rightarrow{I}={Q}\:\therefore\:\mathrm{2}{I}=\frac{\pi}{\mathrm{2}}\Rightarrow{I}=\frac{\pi}{\mathrm{4}}. \\ $$$$ \\ $$
Commented by Yozzia last updated on 22/Aug/16
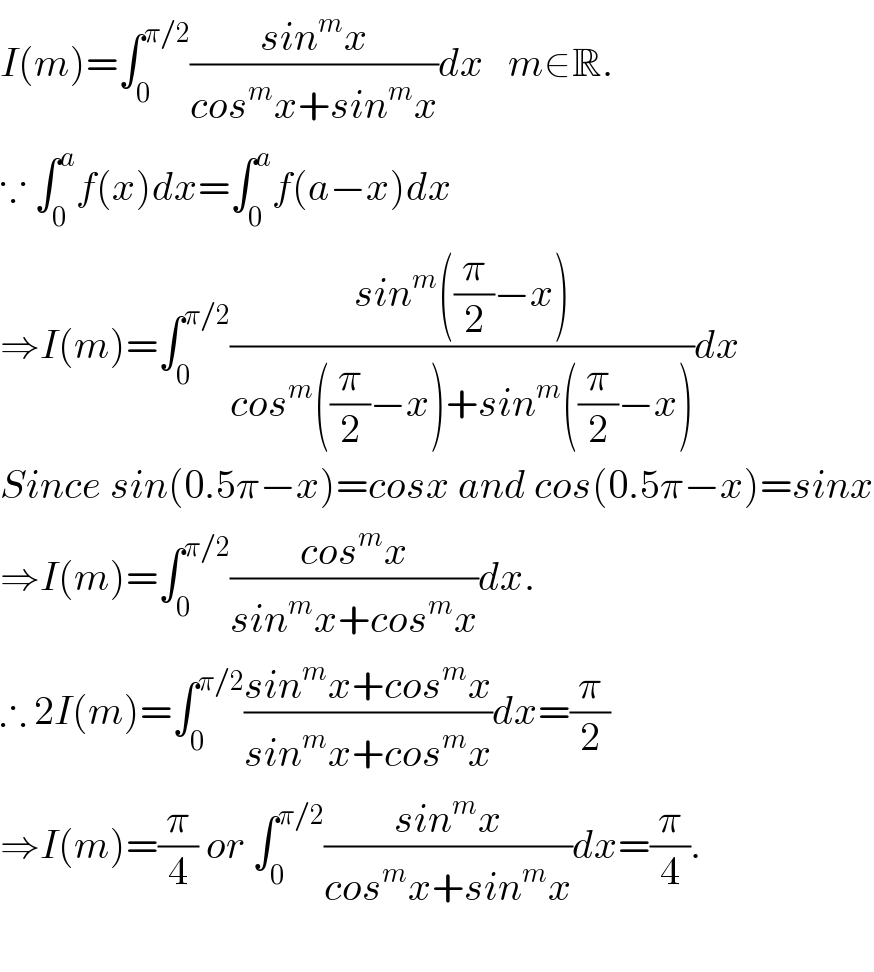
$${I}\left({m}\right)=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sin}^{{m}} {x}}{{cos}^{{m}} {x}+{sin}^{{m}} {x}}{dx}\:\:\:{m}\in\mathbb{R}. \\ $$$$\because\:\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{a}} {f}\left({a}−{x}\right){dx} \\ $$$$\Rightarrow{I}\left({m}\right)=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sin}^{{m}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{{cos}^{{m}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)+{sin}^{{m}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$${Since}\:{sin}\left(\mathrm{0}.\mathrm{5}\pi−{x}\right)={cosx}\:{and}\:{cos}\left(\mathrm{0}.\mathrm{5}\pi−{x}\right)={sinx} \\ $$$$\Rightarrow{I}\left({m}\right)=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{cos}^{{m}} {x}}{{sin}^{{m}} {x}+{cos}^{{m}} {x}}{dx}. \\ $$$$\therefore\:\mathrm{2}{I}\left({m}\right)=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sin}^{{m}} {x}+{cos}^{{m}} {x}}{{sin}^{{m}} {x}+{cos}^{{m}} {x}}{dx}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{I}\left({m}\right)=\frac{\pi}{\mathrm{4}}\:{or}\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{sin}^{{m}} {x}}{{cos}^{{m}} {x}+{sin}^{{m}} {x}}{dx}=\frac{\pi}{\mathrm{4}}. \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 22/Aug/16
$${Wow},\:{thanks}\:{so}\:{much}.\:{i}\:{really}\:{appreciate} \\ $$
