
Question Number 17204 by Arnab Maiti last updated on 02/Jul/17
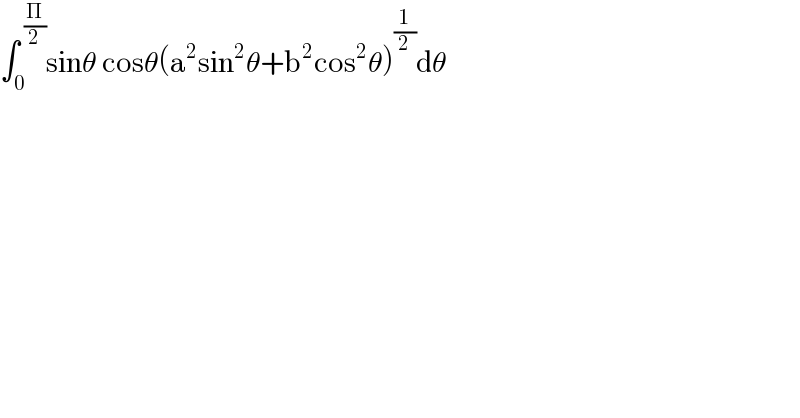
$$\int_{\mathrm{0}} ^{\:\frac{\Pi}{\mathrm{2}}} \mathrm{sin}\theta\:\mathrm{cos}\theta\left(\mathrm{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta+\mathrm{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{d}\theta \\ $$
Answered by prakash jain last updated on 02/Jul/17
![sin^2 θ=((1−cos 2θ)/2) cos^2 θ=((1+cos 2θ)/2) ∫((sin 2θ)/2)((a^2 /2)(1−cos 2θ)+(b^2 /2)(1+cos 2θ))^(1/2) dθ cos 2θ=t⇒−2sin 2θdθ=dt θ=0⇒t=1,θ=(π/2)⇒t=−1 =−(1/(4(√2)))∫_1 ^(−1) (a^2 +b^2 +(b^2 −a^2 )t)^(1/2) dt =(1/(4(√2)))∫_(−1) ^1 (a^2 +b^2 +(b^2 −a^2 )t)^(1/2) dt =(1/(4(b^2 −a^2 )(√2)))∙(2/3)[(a^2 +b^2 +(b^2 −a^2 )t)^(3/2) ]_(−1) ^1 =(((b^3 −a^3 )2(√2))/((b^2 −a^2 )6(√2))) =(((b^3 −a^3 ))/(3(b^2 −a^2 )))](Q17248.png)
$$\mathrm{sin}^{\mathrm{2}} \theta=\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta=\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$$\int\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)+\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)\right)^{\mathrm{1}/\mathrm{2}} {d}\theta \\ $$$$\mathrm{cos}\:\mathrm{2}\theta={t}\Rightarrow−\mathrm{2sin}\:\mathrm{2}\theta{d}\theta={dt} \\ $$$$\theta=\mathrm{0}\Rightarrow{t}=\mathrm{1},\theta=\frac{\pi}{\mathrm{2}}\Rightarrow{t}=−\mathrm{1} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int_{\mathrm{1}} ^{−\mathrm{1}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){t}\right)^{\mathrm{1}/\mathrm{2}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\int_{−\mathrm{1}} ^{\mathrm{1}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){t}\right)^{\mathrm{1}/\mathrm{2}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\left[\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){t}\right)^{\mathrm{3}/\mathrm{2}} \right]_{−\mathrm{1}} ^{\mathrm{1}} \: \\ $$$$=\frac{\left({b}^{\mathrm{3}} −{a}^{\mathrm{3}} \right)\mathrm{2}\sqrt{\mathrm{2}}}{\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\mathrm{6}\sqrt{\mathrm{2}}}\:=\frac{\left({b}^{\mathrm{3}} −{a}^{\mathrm{3}} \right)}{\mathrm{3}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)} \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17
$$\mathrm{Awesome}\:\mathrm{process}\:!\:\mathrm{I}\:\mathrm{really}\:\mathrm{impressed}. \\ $$
Answered by Abbas-Nahi last updated on 03/Jul/17
![let u=a^2 sin^2 θ +b^2 cos^2 θ du=2a^2 sin θcos θ−2b^2 cos θsin θ dθ du=2(a^2 −b^2 )sin θcos θ dθ ⇒sin θcos θ dθ=(1/(2(a^2 −b^2 ))) du =∫_0 ^(Π/2) (1/(2(a^2 −b^2 ))) (u)^(1/2) du =(1/(3(a^2 −b^2 ))) [u^(3/2) ]_0 ^(Π/2) =(1/(3(a^2 −b^2 )))[(√((a^2 sin^2 θ+b^2 cos^2 θ)^(3 ) ))]_0 ^(Π/2) =(1/(3(a^2 −b^2 )))((√((a^2 )^3 )) −(√((b^2 )^3 )) ) =((a^3 −b^3 )/(3(a^2 −b^2 )))](Q17261.png)
$$ \\ $$$$ \\ $$$${let}\:{u}={a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta\:+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\:\: \\ $$$$\:\:\:\:\:{du}=\mathrm{2}{a}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta−\mathrm{2}{b}^{\mathrm{2}} \mathrm{cos}\:\theta\mathrm{sin}\:\theta\:{d}\theta \\ $$$$\:\:\:\:\:\:{du}=\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta\:{d}\theta \\ $$$$\:\:\Rightarrow\mathrm{sin}\:\theta\mathrm{cos}\:\theta\:{d}\theta=\frac{\mathrm{1}}{\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\:{du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\:\left({u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\:\left[{u}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\left[\sqrt{\left({a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta\right)^{\mathrm{3}\:\:} \:\:}\right]_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\left(\sqrt{\left({a}^{\mathrm{2}} \right)^{\mathrm{3}} }\:−\sqrt{\left({b}^{\mathrm{2}} \right)^{\mathrm{3}} }\:\right) \\ $$$$=\frac{{a}^{\mathrm{3}} −{b}^{\mathrm{3}} }{\mathrm{3}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)} \\ $$
Commented by Arnab Maiti last updated on 03/Jul/17

$$\mathrm{Excellent}!!! \\ $$
