
Question Number 167526 by Gbenga last updated on 18/Mar/22

$$\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\sum}}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{1}}\boldsymbol{\mathrm{dn}}=??? \\ $$
Commented by aleks041103 last updated on 18/Mar/22
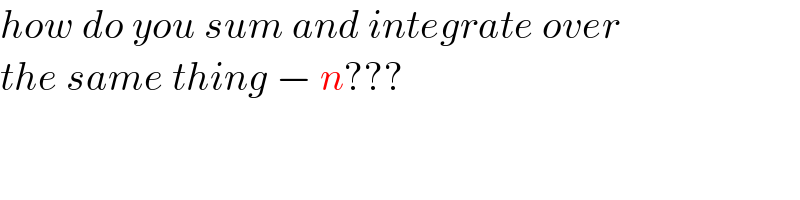
$${how}\:{do}\:{you}\:{sum}\:{and}\:{integrate}\:{over} \\ $$$${the}\:{same}\:{thing}\:−\:{n}??? \\ $$
Answered by MJS_new last updated on 18/Mar/22
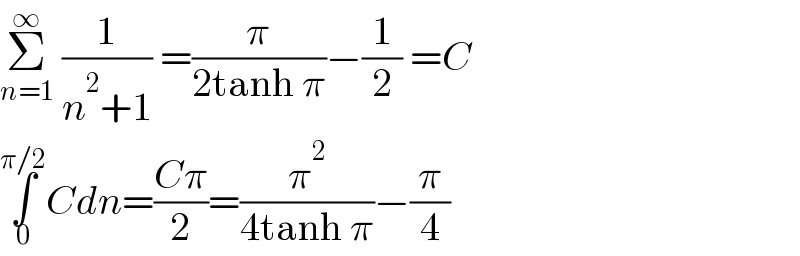
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} +\mathrm{1}}\:=\frac{\pi}{\mathrm{2tanh}\:\pi}−\frac{\mathrm{1}}{\mathrm{2}}\:={C} \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}{Cdn}=\frac{{C}\pi}{\mathrm{2}}=\frac{\pi^{\mathrm{2}} }{\mathrm{4tanh}\:\pi}−\frac{\pi}{\mathrm{4}} \\ $$
