
Question Number 60240 by ANTARES VY last updated on 19/May/19
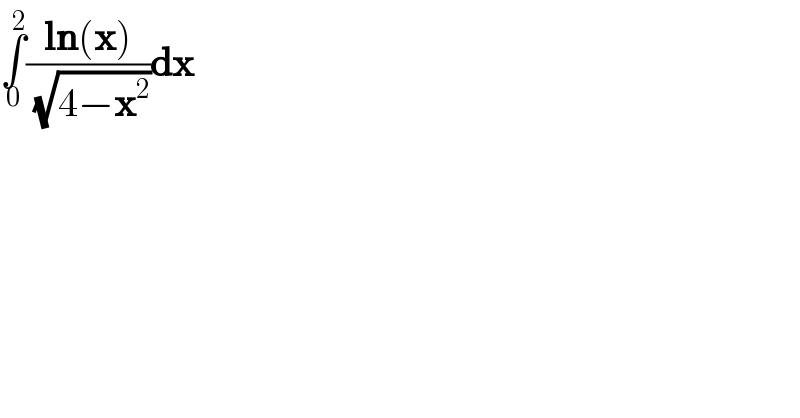
$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\frac{\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)}{\sqrt{\mathrm{4}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}\boldsymbol{\mathrm{dx}} \\ $$
Commented by maxmathsup by imad last updated on 19/May/19
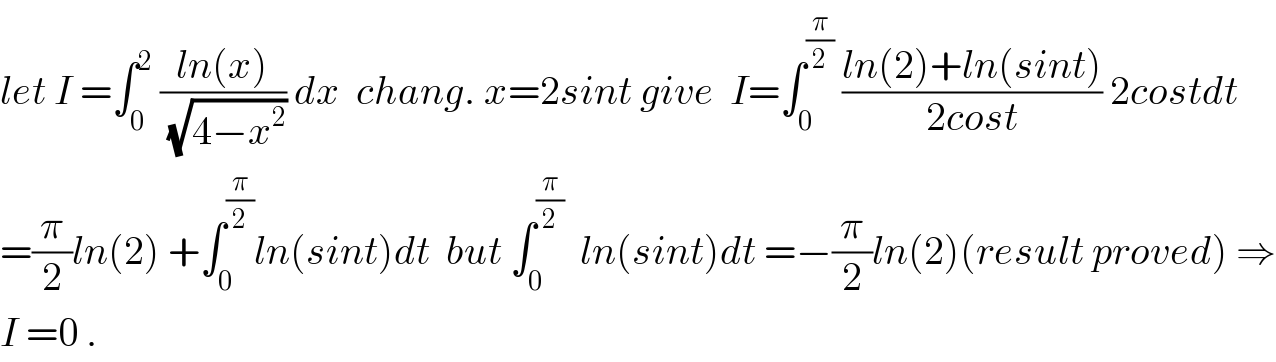
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{{ln}\left({x}\right)}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\:{dx}\:\:{chang}.\:{x}=\mathrm{2}{sint}\:{give}\:\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{ln}\left(\mathrm{2}\right)+{ln}\left({sint}\right)}{\mathrm{2}{cost}}\:\mathrm{2}{costdt} \\ $$$$=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sint}\right){dt}\:\:{but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{ln}\left({sint}\right){dt}\:=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\left({result}\:{proved}\right)\:\Rightarrow \\ $$$${I}\:=\mathrm{0}\:. \\ $$
