
Question Number 94948 by rb222 last updated on 22/May/20
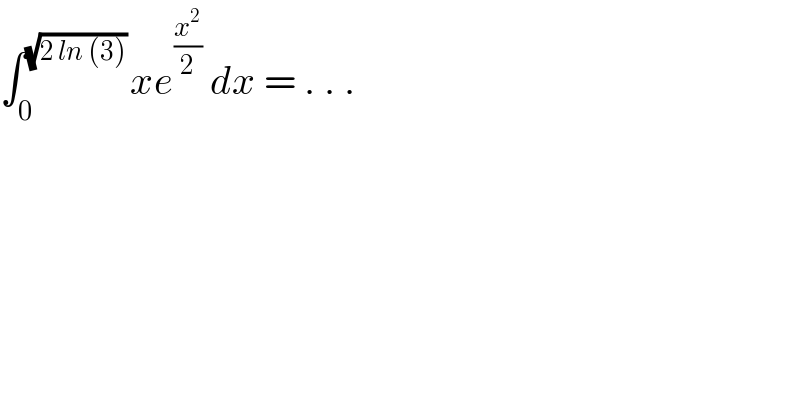
$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}\:{ln}\:\left(\mathrm{3}\right)}\:} {xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:{dx}\:=\:.\:.\:. \\ $$
Commented by Tony Lin last updated on 22/May/20
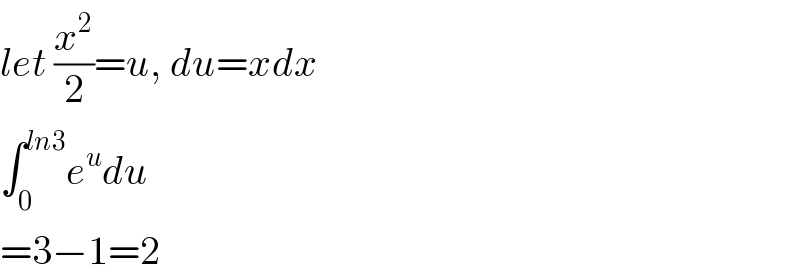
$${let}\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}={u},\:{du}={xdx} \\ $$$$\int_{\mathrm{0}} ^{{ln}\mathrm{3}} {e}^{{u}} {du} \\ $$$$=\mathrm{3}−\mathrm{1}=\mathrm{2} \\ $$
Commented by rb222 last updated on 22/May/20

$${thanks}\:{sir} \\ $$
Commented by john santu last updated on 22/May/20
![∫ x.e^(x^2 /2) dx = ∫e^((1/2)x^2 ) d((1/2)x^2 ) = e^((1/2)x^2 ) then ∫_0 ^(√(2 ln(3))) x.e^((1/2)x^2 ) dx = [ e^((1/2)x^2 ) ]_( 0) ^(√(2 ln(3))) = e^(ln(3)) −e^0 = 3−1 = 2](Q94959.png)
$$\int\:{x}.{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:{dx}\:=\:\int{e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \:{d}\left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right) \\ $$$$=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \\ $$$${then}\:\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{2}\:\mathrm{ln}\left(\mathrm{3}\right)}} {\int}}{x}.{e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \:{dx}\:=\:\left[\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \:\right]_{\:\mathrm{0}} ^{\sqrt{\mathrm{2}\:\mathrm{ln}\left(\mathrm{3}\right)}} \\ $$$$=\:{e}^{\mathrm{ln}\left(\mathrm{3}\right)} −\mathrm{e}^{\mathrm{0}} \:=\:\mathrm{3}−\mathrm{1}\:=\:\mathrm{2} \\ $$
Answered by niroj last updated on 22/May/20
![∫_0 ^( (√(2In(3)))) x e^(x^2 /2) dx Put, (x^2 /2)= t x^2 = 2t 2xdx=2dt xdx=dt If x=(√(2ln(3))) ⇒t =((2In(3))/2)=In(3) If x=0 ⇒ t=0 ∫_0 ^( In(3)) e^t dt = [ e^t ]_0 ^(ln(3)) =e^(ln(3)) −e^0 =3−1= 2 //.](Q94950.png)
$$\:\:\int_{\mathrm{0}} ^{\:\sqrt{\mathrm{2}{In}\left(\mathrm{3}\right)}} \mathrm{x}\:\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \mathrm{dx} \\ $$$$\:\:\mathrm{Put},\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} =\:\mathrm{2t} \\ $$$$\:\:\:\:\:\:\mathrm{2xdx}=\mathrm{2dt} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{xdx}=\mathrm{dt} \\ $$$$\:\:\:\:\:\:\mathrm{If}\:\mathrm{x}=\sqrt{\mathrm{2ln}\left(\mathrm{3}\right)}\:\:\Rightarrow\mathrm{t}\:=\frac{\mathrm{2In}\left(\mathrm{3}\right)}{\mathrm{2}}=\mathrm{In}\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\mathrm{If}\:\mathrm{x}=\mathrm{0}\:\Rightarrow\:\mathrm{t}=\mathrm{0} \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{In}\left(\mathrm{3}\right)} \:\mathrm{e}^{\mathrm{t}} \mathrm{dt} \\ $$$$\:=\:\left[\:\mathrm{e}^{\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{3}\right)} \\ $$$$\:=\mathrm{e}^{\mathrm{ln}\left(\mathrm{3}\right)} −\mathrm{e}^{\mathrm{0}} \\ $$$$\:\:=\mathrm{3}−\mathrm{1}=\:\mathrm{2}\://. \\ $$$$ \\ $$
Commented by rb222 last updated on 22/May/20

$${thanks}\:{sir} \\ $$
Commented by niroj last updated on 22/May/20
��
Commented by peter frank last updated on 22/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
