
Question Number 194662 by SANOGO last updated on 12/Jul/23
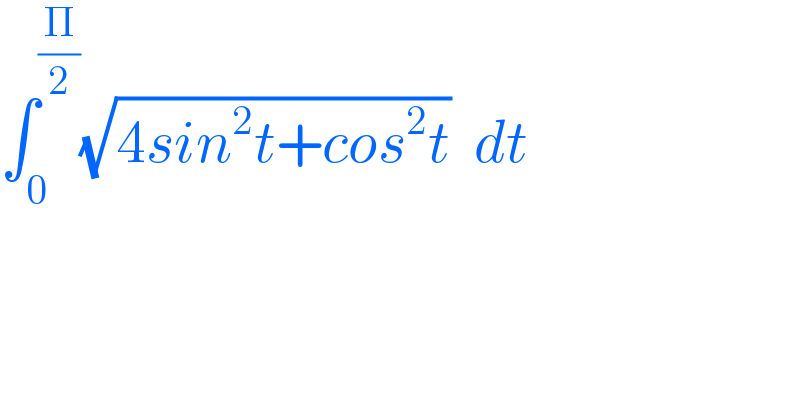
$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \sqrt{\mathrm{4}{sin}^{\mathrm{2}} {t}+{cos}^{\mathrm{2}} {t}}\:\:{dt} \\ $$
Commented by Frix last updated on 12/Jul/23
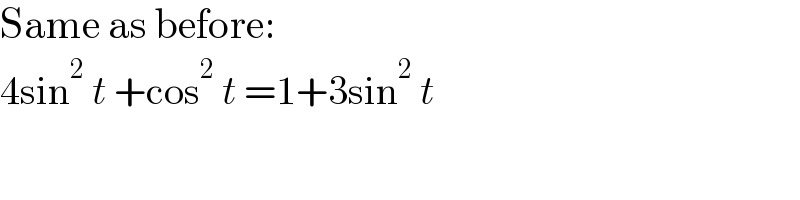
$$\mathrm{Same}\:\mathrm{as}\:\mathrm{before}: \\ $$$$\mathrm{4sin}^{\mathrm{2}} \:{t}\:+\mathrm{cos}^{\mathrm{2}} \:{t}\:=\mathrm{1}+\mathrm{3sin}^{\mathrm{2}} \:{t} \\ $$
Commented by SANOGO last updated on 12/Jul/23
$${ok}\:{thank}\:{you} \\ $$
