
Question Number 90784 by jagoll last updated on 26/Apr/20
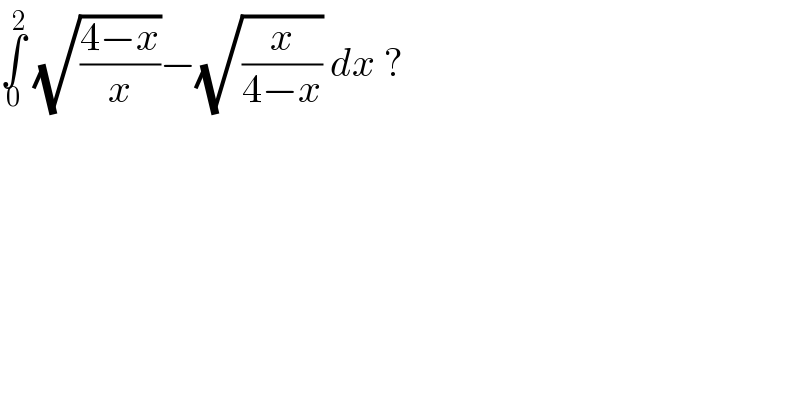
$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\sqrt{\frac{\mathrm{4}−{x}}{{x}}}−\sqrt{\frac{{x}}{\mathrm{4}−{x}}}\:{dx}\:? \\ $$
Commented by jagoll last updated on 26/Apr/20
![∫_0 ^2 ((((√(4−x)))^2 −((√x))^2 )/((√x) ((√(4−x)) ) )) = ∫_0 ^2 ((4−2x)/(√(4x−x^2 ))) dx = ∫_0 ^2 ((d(4x−x^2 ))/(√(4x−x^2 ))) = 2 (√(4x−x^2 )) ]_0 ^2 = 2 (√(8−4)) = 2×2 = 4](Q90785.png)
$$\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\left(\sqrt{\mathrm{4}−{x}}\right)^{\mathrm{2}} −\left(\sqrt{{x}}\right)^{\mathrm{2}} }{\sqrt{{x}}\:\left(\sqrt{\mathrm{4}−{x}}\:\right)\:}\:=\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{4}−\mathrm{2}{x}}{\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }}\:{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{{d}\left(\mathrm{4}{x}−{x}^{\mathrm{2}} \right)}{\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }} \\ $$$$\left.=\:\mathrm{2}\:\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }\:\right]_{\mathrm{0}} ^{\mathrm{2}} \:=\:\mathrm{2}\:\sqrt{\mathrm{8}−\mathrm{4}} \\ $$$$=\:\mathrm{2}×\mathrm{2}\:=\:\mathrm{4} \\ $$
Commented by abdomathmax last updated on 27/Apr/20
![A=∫_0 ^2 (√((4−x)/x))dx−∫_0 ^2 (√(x/(4−x)))dx =H−K changement (√((4−x)/x))=t give ((4−x)/x)=t^2 ⇒ 4−x =t^2 x ⇒(1+t^2 )x =4 ⇒x=(4/(t^2 +1)) ⇒ H =−∫_1 ^(+∞) t×(−((4(2t))/((t^2 +1)^2 )))dt =8 ∫_1 ^(+∞) ((t^2 +1−1)/((t^2 +1)^2 ))dt =8 ∫_1 ^(+∞) (dt/(1+t^2 ))−8∫_1 ^(+∞) (dt/((1+t^2 )^2 )) ∫_1 ^(+∞) (dt/(1+t^2 )) =(π/2)−(π/4) =(π/4) ∫_1 ^(+∞) (dt/((1+t^2 )^2 )) =_(t=tanθ) ∫_(π/4) ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ =∫_(π/4) ^(π/2) cos^2 θ =(1/2)∫_(π/4) ^(π/2) (1+cos(2θ))dθ =(1/2)×(π/4) +(1/4)[sin(2θ)]_(π/4) ^(π/2) =(π/8)+(1/4)(−1) ⇒ H =2π−8{(π/8)−(1/4)}=π+2 and K=∫_0 ^2 (√(x/(4−x)))dx we do the changement (√(x/(4−x)))=t ⇒ (x/(4−x)) =t^2 ⇒x =4t^2 −t^2 x ⇒(1+t^2 )x =4t^2 ⇒ x =((4t^2 )/(t^2 +1)) ⇒(dx/dt) =((8t(t^2 +1)−4t^2 (2t))/((t^2 +1)^2 ))=((8t)/((t^2 +1)^2 )) K =∫_0 ^1 t×((8t)/((t^2 +1)^2 ))dt =8 ∫_0 ^1 ((t^2 +1−1)/((t^2 +1)^2 ))dt =8 ∫_0 ^1 (dt/(t^2 +1))−8 ∫_0 ^1 (dt/((t^2 +1)^2 )) =8×(π/4)−8{ ∫_0 ^(π/4) (((1+tan^2 θ)dθ)/((1+tan^2 θ)^2 ))} (t=tanθ) =2π −8{∫_0 ^(π/4) cos^2 θ dθ} =2π−4∫_0 ^(π/4) (1+cos(2θ))dθ =π−2 [sin(2θ)]_0 ^(π/4) =π−2{1} =π−2 A =H−K =π +2−π +2 =4](Q90939.png)
$${A}=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{\mathrm{4}−{x}}{{x}}}{dx}−\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{{x}}{\mathrm{4}−{x}}}{dx}\:={H}−{K} \\ $$$${changement}\:\sqrt{\frac{\mathrm{4}−{x}}{{x}}}={t}\:{give}\:\frac{\mathrm{4}−{x}}{{x}}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{4}−{x}\:={t}^{\mathrm{2}} {x}\:\Rightarrow\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}\:=\mathrm{4}\:\Rightarrow{x}=\frac{\mathrm{4}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${H}\:=−\int_{\mathrm{1}} ^{+\infty} {t}×\left(−\frac{\mathrm{4}\left(\mathrm{2}{t}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right){dt} \\ $$$$=\mathrm{8}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=\mathrm{8}\:\int_{\mathrm{1}} ^{+\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−\mathrm{8}\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{{t}={tan}\theta} \:\:\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}}\left(−\mathrm{1}\right)\:\Rightarrow \\ $$$${H}\:=\mathrm{2}\pi−\mathrm{8}\left\{\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}\right\}=\pi+\mathrm{2}\:\:\:{and}\:{K}=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{{x}}{\mathrm{4}−{x}}}{dx} \\ $$$${we}\:{do}\:{the}\:{changement}\:\sqrt{\frac{{x}}{\mathrm{4}−{x}}}={t}\:\Rightarrow \\ $$$$\frac{{x}}{\mathrm{4}−{x}}\:={t}^{\mathrm{2}} \:\Rightarrow{x}\:=\mathrm{4}{t}^{\mathrm{2}} −{t}^{\mathrm{2}} {x}\:\Rightarrow\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}\:=\mathrm{4}{t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}\:=\frac{\mathrm{4}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\frac{{dx}}{{dt}}\:=\frac{\mathrm{8}{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{4}{t}^{\mathrm{2}} \left(\mathrm{2}{t}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{8}{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${K}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}×\frac{\mathrm{8}{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=\mathrm{8}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{8}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}−\mathrm{8}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{8}×\frac{\pi}{\mathrm{4}}−\mathrm{8}\left\{\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\right\}\:\:\left({t}={tan}\theta\right) \\ $$$$=\mathrm{2}\pi\:−\mathrm{8}\left\{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}^{\mathrm{2}} \theta\:{d}\theta\right\} \\ $$$$=\mathrm{2}\pi−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\pi−\mathrm{2}\:\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\pi−\mathrm{2}\left\{\mathrm{1}\right\}\:=\pi−\mathrm{2} \\ $$$${A}\:={H}−{K}\:=\pi\:+\mathrm{2}−\pi\:+\mathrm{2}\:=\mathrm{4} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
