
Question Number 150678 by krauss last updated on 14/Aug/21
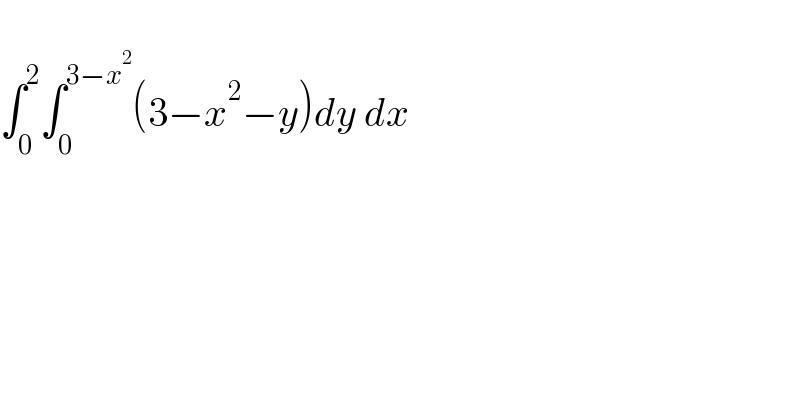
$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{3}−{x}^{\mathrm{2}} } \left(\mathrm{3}−{x}^{\mathrm{2}} −{y}\right){dy}\:{dx} \\ $$
Answered by Ar Brandon last updated on 14/Aug/21
![I=∫_0 ^2 ∫_0 ^(3−x^2 ) (3−x^2 −y^2 )dydx=∫_0 ^2 [3y−x^2 y−(y^3 /3)]_0 ^(3−x^2 ) dx =∫_0 ^2 (3(3−x^2 )−x^2 (3−x^2 )−(((3−x^2 )^3 )/3))dx You may proceed by expanding and integrating.](Q150706.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{3}−{x}^{\mathrm{2}} } \left(\mathrm{3}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right){dydx}=\int_{\mathrm{0}} ^{\mathrm{2}} \left[\mathrm{3}{y}−{x}^{\mathrm{2}} {y}−\frac{{y}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{3}−{x}^{\mathrm{2}} } {dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{3}\left(\mathrm{3}−{x}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} \left(\mathrm{3}−{x}^{\mathrm{2}} \right)−\frac{\left(\mathrm{3}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} }{\mathrm{3}}\right){dx} \\ $$$$\mathrm{You}\:\mathrm{may}\:\mathrm{proceed}\:\mathrm{by}\:\mathrm{expanding}\:\mathrm{and}\:\mathrm{integrating}. \\ $$
Answered by tabata last updated on 15/Aug/21
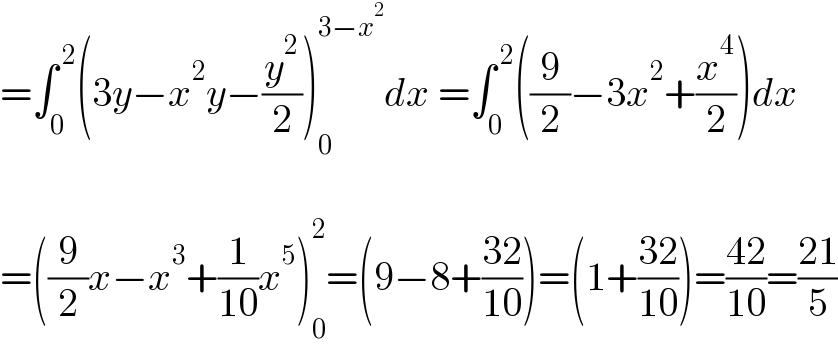
$$=\int_{\mathrm{0}} ^{\:\mathrm{2}} \left(\mathrm{3}{y}−{x}^{\mathrm{2}} {y}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\right)_{\mathrm{0}} ^{\mathrm{3}−{x}^{\mathrm{2}} } {dx}\:=\int_{\mathrm{0}} ^{\:\mathrm{2}} \left(\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{3}{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{2}}\right){dx} \\ $$$$ \\ $$$$=\left(\frac{\mathrm{9}}{\mathrm{2}}{x}−{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{10}}{x}^{\mathrm{5}} \right)_{\mathrm{0}} ^{\mathrm{2}} =\left(\mathrm{9}−\mathrm{8}+\frac{\mathrm{32}}{\mathrm{10}}\right)=\left(\mathrm{1}+\frac{\mathrm{32}}{\mathrm{10}}\right)=\frac{\mathrm{42}}{\mathrm{10}}=\frac{\mathrm{21}}{\mathrm{5}} \\ $$
