
Question Number 116491 by bemath last updated on 04/Oct/20
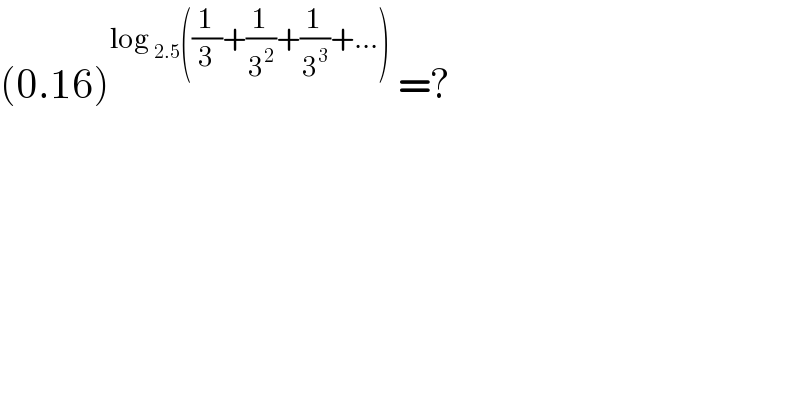
$$\left(\mathrm{0}.\mathrm{16}\right)^{\mathrm{log}\:_{\mathrm{2}.\mathrm{5}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+...\right)} \:=? \\ $$
Answered by bobhans last updated on 04/Oct/20
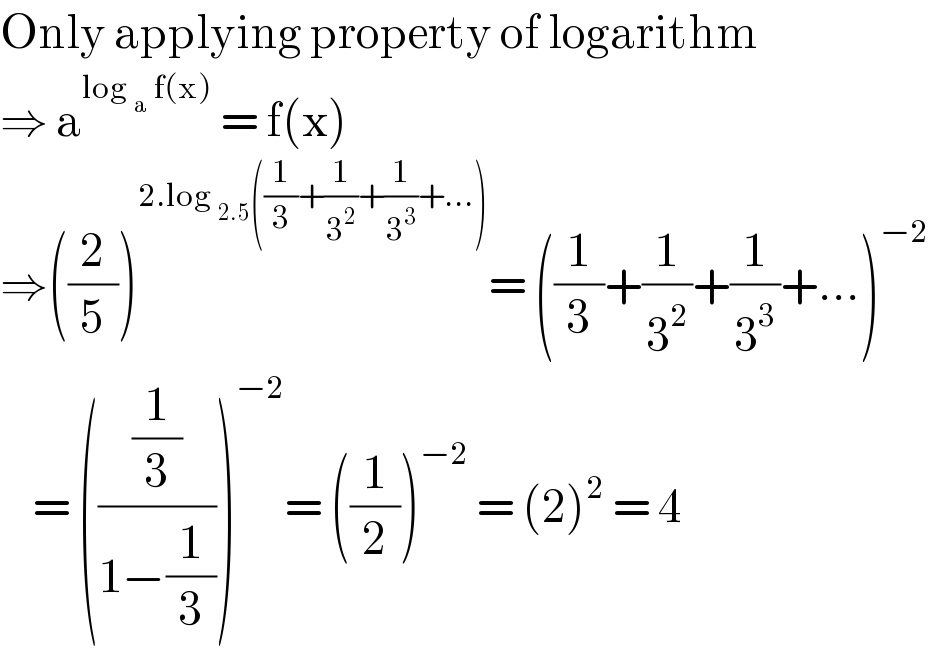
$$\mathrm{Only}\:\mathrm{applying}\:\mathrm{property}\:\mathrm{of}\:\mathrm{logarithm} \\ $$$$\Rightarrow\:\mathrm{a}^{\mathrm{log}\:_{\mathrm{a}} \:\mathrm{f}\left(\mathrm{x}\right)} \:=\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}.\mathrm{log}\:_{\mathrm{2}.\mathrm{5}} \left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+...\right)} =\:\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }+...\right)^{−\mathrm{2}} \\ $$$$\:\:\:\:=\:\left(\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\right)^{−\mathrm{2}} =\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\mathrm{2}} \:=\:\left(\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{4} \\ $$
