Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 207054 by Ghisom last updated on 05/May/24

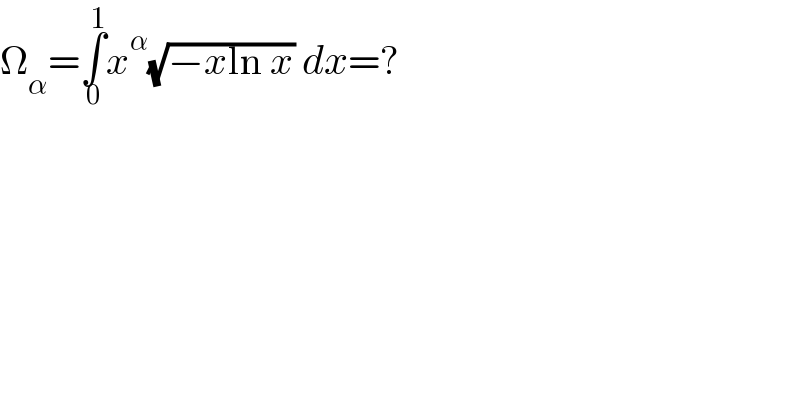
Ω_α =∫_0 ^1 x^α (√(−xln x)) dx=?

$$\Omega_{\alpha} =\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\alpha} \sqrt{−{x}\mathrm{ln}\:{x}}\:{dx}=? \\ $$

Answered by Frix last updated on 05/May/24

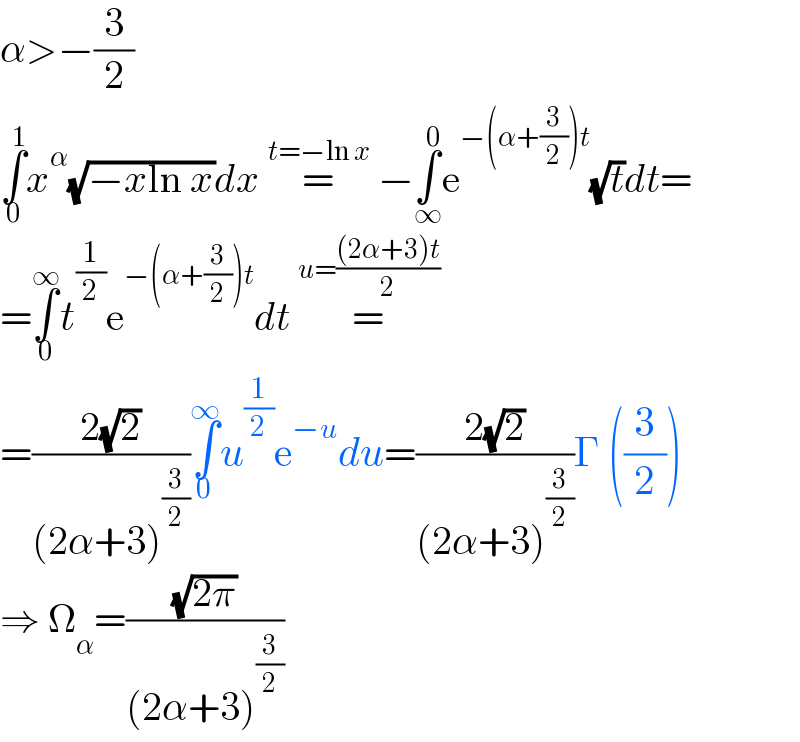
α>−(3/2) ∫_0 ^1 x^α (√(−xln x))dx =^(t=−ln x) −∫_∞ ^0 e^(−(α+(3/2))t) (√t)dt= =∫_0 ^∞ t^(1/2) e^(−(α+(3/2))t) dt =^(u=(((2α+3)t)/2)) =((2(√2))/((2α+3)^(3/2) ))∫_0 ^∞ u^(1/2) e^(−u) du=((2(√2))/((2α+3)^(3/2) ))Γ ((3/2)) ⇒ Ω_α =((√(2π))/((2α+3)^(3/2) ))

$$\alpha>−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\alpha} \sqrt{−{x}\mathrm{ln}\:{x}}{dx}\:\overset{{t}=−\mathrm{ln}\:{x}} {=}\:−\underset{\infty} {\overset{\mathrm{0}} {\int}}\mathrm{e}^{−\left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right){t}} \sqrt{{t}}{dt}= \\ $$$$=\underset{\mathrm{0}} {\overset{\infty} {\int}}{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{e}^{−\left(\alpha+\frac{\mathrm{3}}{\mathrm{2}}\right){t}} {dt}\:\overset{{u}=\frac{\left(\mathrm{2}\alpha+\mathrm{3}\right){t}}{\mathrm{2}}} {=} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{2}\alpha+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\underset{\mathrm{0}} {\overset{\infty} {\int}}{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{e}^{−{u}} {du}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\left(\mathrm{2}\alpha+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\Gamma\:\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\Omega_{\alpha} =\frac{\sqrt{\mathrm{2}\pi}}{\left(\mathrm{2}\alpha+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$

Commented by Ghisom last updated on 05/May/24

thank you I found the 1^(st) substitution but I did not see the shape of the Γ−function

$$\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{substitution}\:\mathrm{but}\:\mathrm{I}\:\mathrm{did}\:\mathrm{not} \\ $$$$\mathrm{see}\:\mathrm{the}\:\mathrm{shape}\:\mathrm{of}\:\mathrm{the}\:\Gamma−\mathrm{function} \\ $$

Commented by Frix last updated on 05/May/24

�� I remember this "trick" from long ago because it surprised me...

Terms of Service

Privacy Policy

Contact: info@tinkutara.com