
Question Number 113110 by gopikrishnan last updated on 11/Sep/20
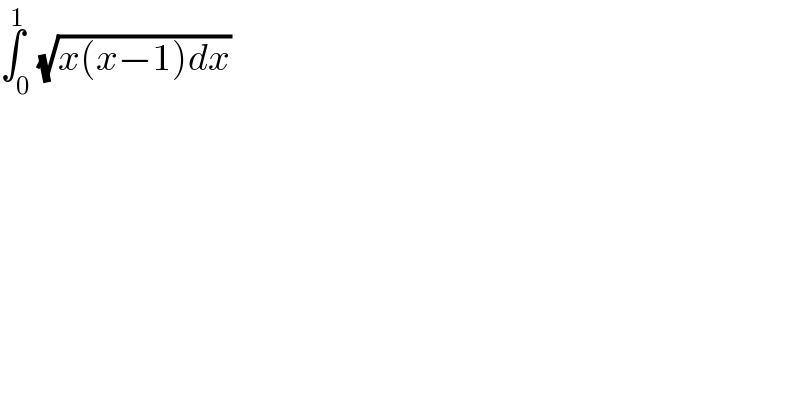
$$\overset{\mathrm{1}} {\int}_{\mathrm{0}} \sqrt{{x}\left({x}−\mathrm{1}\right){dx}} \\ $$
Commented by 1549442205PVT last updated on 11/Sep/20
![The function (√(x(x−1))) is defined on set X=(−∞,0]∪[1,+∞) and isn′t defined on (0,1),so ∫_0 ^1 (√(x(x−1)dx)) don′t exist You should see your question again](Q113125.png)
$$\mathrm{The}\:\mathrm{function}\:\sqrt{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{on} \\ $$$$\mathrm{set}\:\mathrm{X}=\left(−\infty,\mathrm{0}\right]\cup\left[\mathrm{1},+\infty\right)\:\mathrm{and}\:\mathrm{isn}'\mathrm{t} \\ $$$$\mathrm{defined}\:\mathrm{on}\:\left(\mathrm{0},\mathrm{1}\right),\mathrm{so}\:\overset{\mathrm{1}} {\int}_{\mathrm{0}} \sqrt{{x}\left({x}−\mathrm{1}\right){dx}} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{exist} \\ $$$$\boldsymbol{\mathrm{You}}\:\boldsymbol{\mathrm{should}}\:\boldsymbol{\mathrm{see}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{question}}\:\boldsymbol{\mathrm{again}} \\ $$
Commented by gopikrishnan last updated on 11/Sep/20

$${ok}\:{sir} \\ $$
Answered by MJS_new last updated on 11/Sep/20
![I think you mean ∫(√(x(x−1))) dx ∫(√(x(x−1)))dx= [t=(√(x/(x−1))) → dx=−2(√(x(x−1)^3 ))dt] =−2∫(t^2 /((t^2 −1)^3 ))dx= [Ostrogradski′s method] =((t(t^2 +1))/(4(t^2 −1)^2 ))+(1/4)∫(dt/(t^2 −1))= =((t(t^2 +1))/(4(t^2 −1)^2 ))+(1/8)ln ((t−1)/(t+1)) = =(1/4)(2x−1)(√(x(x−1)))+(1/4)ln ((√x)−(√(x−1))) +C ⇒ ∫_0 ^1 (√(x(x−1)))dx=(π/8)i](Q113145.png)
$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{mean}\:\int\sqrt{{x}\left({x}−\mathrm{1}\right)}\:{dx} \\ $$$$\int\sqrt{{x}\left({x}−\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{{x}}{{x}−\mathrm{1}}}\:\rightarrow\:{dx}=−\mathrm{2}\sqrt{{x}\left({x}−\mathrm{1}\right)^{\mathrm{3}} }{dt}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{method}\right] \\ $$$$=\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}= \\ $$$$=\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\sqrt{{x}}−\sqrt{{x}−\mathrm{1}}\right)\:+{C} \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{{x}\left({x}−\mathrm{1}\right)}{dx}=\frac{\pi}{\mathrm{8}}\mathrm{i} \\ $$
Commented by gopikrishnan last updated on 11/Sep/20

$${Thank}\:{u}\:{sir} \\ $$
Answered by abdomsup last updated on 11/Sep/20
![i think is ∫_0 ^1 (√(x(1−x)))dx we do the changement (√x)=t ⇒ I =∫_0 ^1 t(√(1−t^2 ))(2t)dt =2∫_0 ^1 t^2 (√(1−t^2 ))dt =_(t=sinθ) 2∫_0 ^(π/2) sin^2 θ cosθ cosθ dθ =2∫_0 ^(π/2) ((1/2)sin(2θ))^2 dθ =(1/2)∫_0 ^(π/2) ((1−cos(4θ))/2) dθ =(π/8) −(1/4)[(1/4)sin(4θ)]_0 ^(π/2) =(π/8)−0 ⇒I=(π/8)](Q113197.png)
$${i}\:{think}\:\:{is}\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}\left(\mathrm{1}−{x}\right)}{dx} \\ $$$${we}\:{do}\:{the}\:{changement}\:\sqrt{{x}}={t}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}} \sqrt{\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=_{{t}={sin}\theta} \:\:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}^{\mathrm{2}} \theta\:{cos}\theta\:{cos}\theta\:{d}\theta \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}} \:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}−{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}\:{d}\theta \\ $$$$=\frac{\pi}{\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{4}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{8}}−\mathrm{0} \\ $$$$\Rightarrow{I}=\frac{\pi}{\mathrm{8}} \\ $$
Commented by gopikrishnan last updated on 11/Sep/20

$${Thank}\:{u}\:{sir} \\ $$
