
Question Number 160979 by amin96 last updated on 10/Dec/21
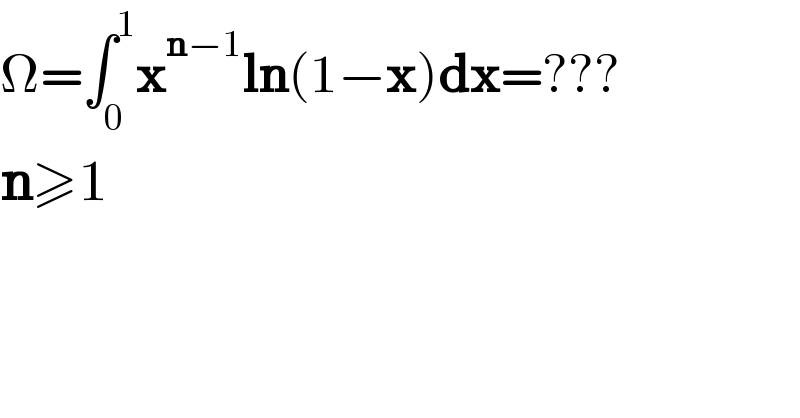
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}−\mathrm{1}} \boldsymbol{\mathrm{ln}}\left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}}=???\:\:\: \\ $$$$\boldsymbol{\mathrm{n}}\geqslant\mathrm{1} \\ $$
Answered by qaz last updated on 10/Dec/21
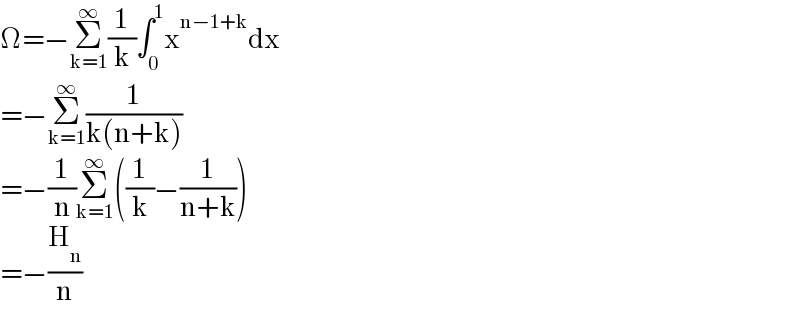
$$\Omega=−\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}+\mathrm{k}} \mathrm{dx} \\ $$$$=−\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{n}+\mathrm{k}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\right) \\ $$$$=−\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}} \\ $$
Commented by amin96 last updated on 10/Dec/21

$${bravooooo} \\ $$
