
Question Number 171744 by mnjuly1970 last updated on 20/Jun/22
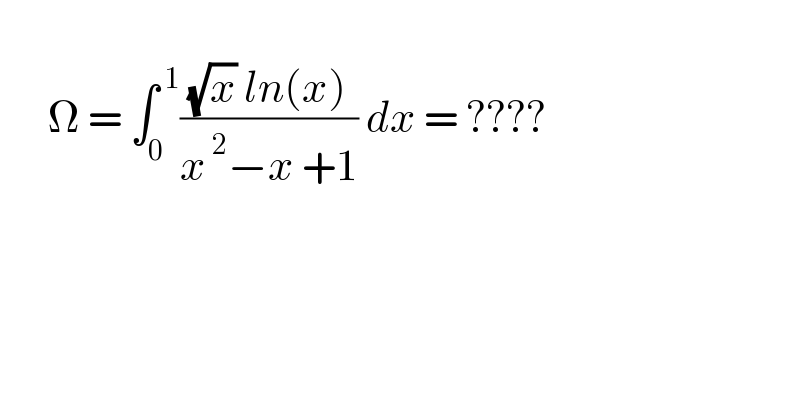
$$ \\ $$$$\:\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\sqrt{{x}}\:{ln}\left({x}\right)}{{x}^{\:\mathrm{2}} −{x}\:+\mathrm{1}}\:{dx}\:=\:???? \\ $$
Answered by Mathspace last updated on 21/Jun/22
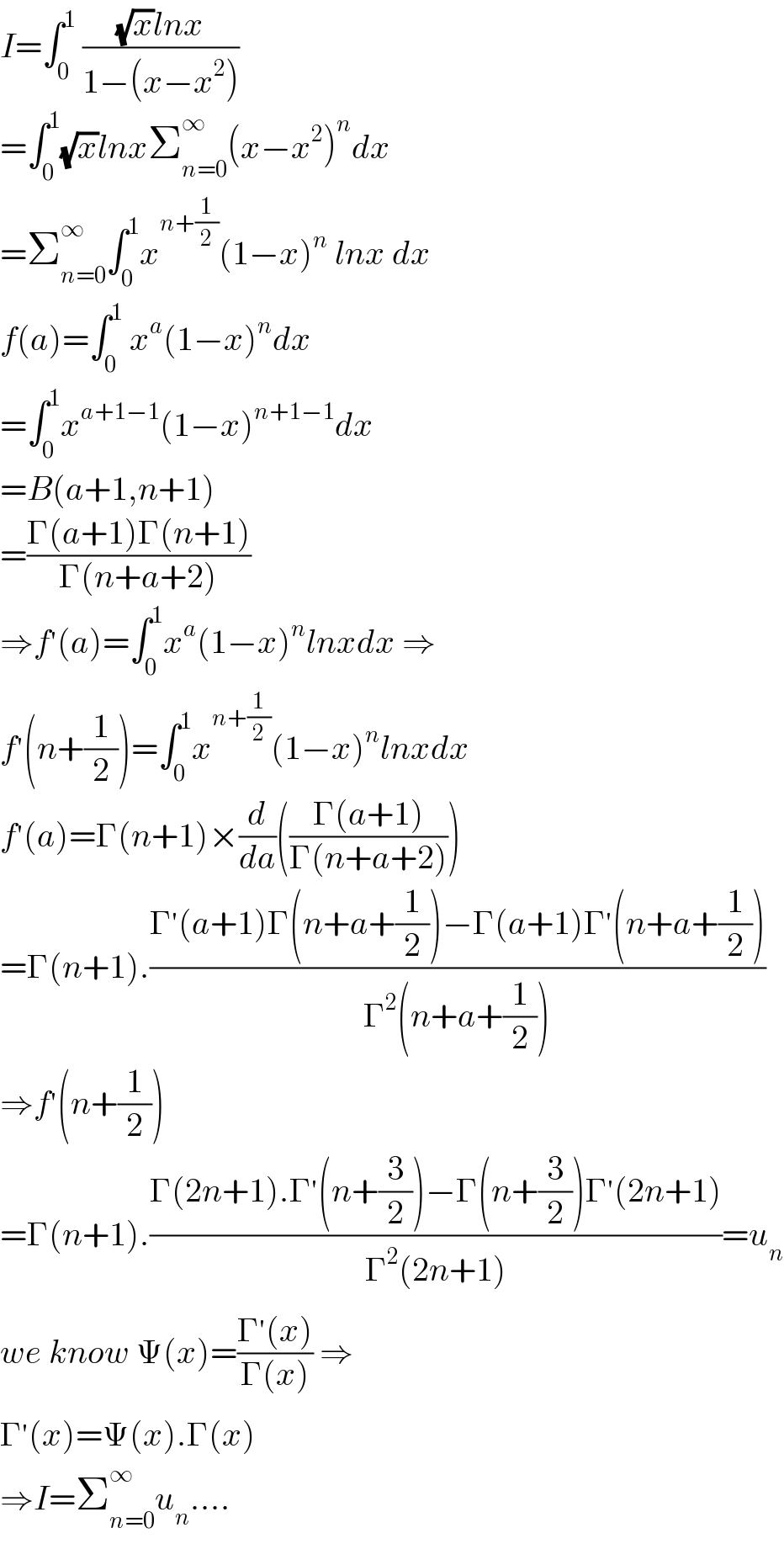
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{{x}}{lnx}}{\mathrm{1}−\left({x}−{x}^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{lnx}\sum_{{n}=\mathrm{0}} ^{\infty} \left({x}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{x}\right)^{{n}} \:{lnx}\:{dx} \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{a}} \left(\mathrm{1}−{x}\right)^{{n}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}+\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}−\mathrm{1}} {dx} \\ $$$$={B}\left({a}+\mathrm{1},{n}+\mathrm{1}\right) \\ $$$$=\frac{\Gamma\left({a}+\mathrm{1}\right)\Gamma\left({n}+\mathrm{1}\right)}{\Gamma\left({n}+{a}+\mathrm{2}\right)} \\ $$$$\Rightarrow{f}^{'} \left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} \left(\mathrm{1}−{x}\right)^{{n}} {lnxdx}\:\Rightarrow \\ $$$${f}^{'} \left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{x}\right)^{{n}} {lnxdx} \\ $$$${f}^{'} \left({a}\right)=\Gamma\left({n}+\mathrm{1}\right)×\frac{{d}}{{da}}\left(\frac{\Gamma\left({a}+\mathrm{1}\right)}{\Gamma\left({n}+{a}+\mathrm{2}\right)}\right) \\ $$$$=\Gamma\left({n}+\mathrm{1}\right).\frac{\Gamma^{'} \left({a}+\mathrm{1}\right)\Gamma\left({n}+{a}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\Gamma\left({a}+\mathrm{1}\right)\Gamma^{'} \left({n}+{a}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left({n}+{a}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow{f}^{'} \left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\Gamma\left({n}+\mathrm{1}\right).\frac{\Gamma\left(\mathrm{2}{n}+\mathrm{1}\right).\Gamma^{'} \left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)−\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma^{'} \left(\mathrm{2}{n}+\mathrm{1}\right)}{\Gamma^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)}={u}_{{n}} \\ $$$${we}\:{know}\:\Psi\left({x}\right)=\frac{\Gamma^{'} \left({x}\right)}{\Gamma\left({x}\right)}\:\Rightarrow \\ $$$$\Gamma^{'} \left({x}\right)=\Psi\left({x}\right).\Gamma\left({x}\right) \\ $$$$\Rightarrow{I}=\sum_{{n}=\mathrm{0}} ^{\infty} {u}_{{n}} .... \\ $$
