Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 208083 by nachosam last updated on 04/Jun/24

∫_([0,∞]) ((1/x))^(ln(x)) dx

$$\int_{\left[\mathrm{0},\infty\right]} \left(\frac{\mathrm{1}}{{x}}\right)^{{ln}\left({x}\right)} {dx} \\ $$$$ \\ $$

Answered by Saiki last updated on 04/Jun/24

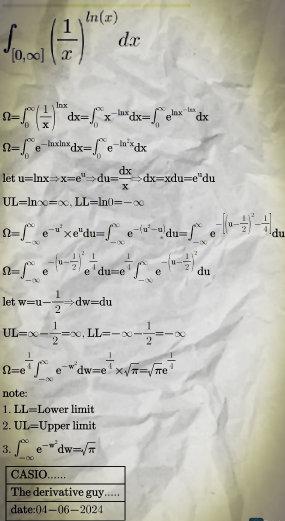
Answered by mathzup last updated on 05/Jun/24

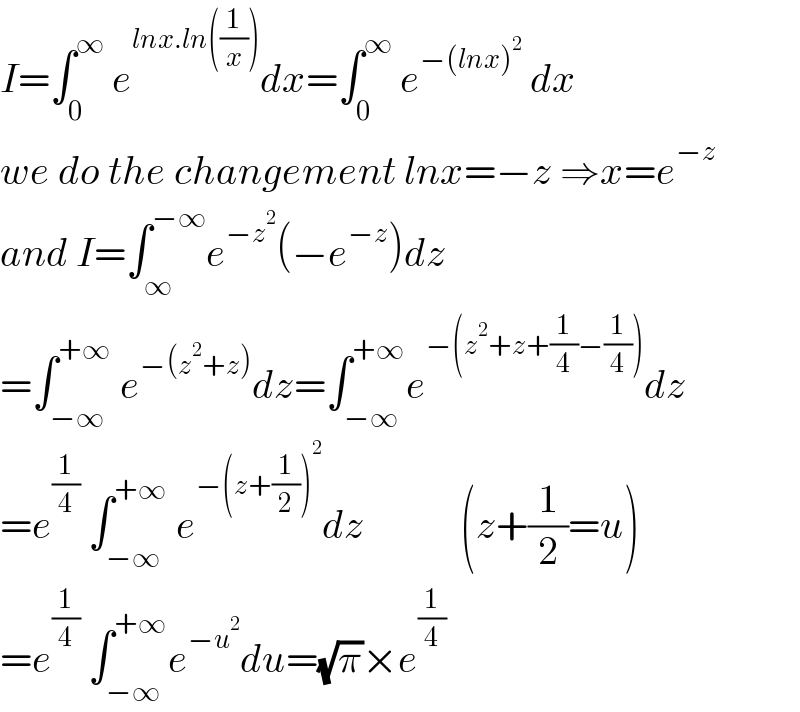
I=∫_0 ^∞ e^(lnx.ln((1/x))) dx=∫_0 ^∞ e^(−(lnx)^2 ) dx we do the changement lnx=−z ⇒x=e^(−z) and I=∫_∞ ^(−∞) e^(−z^2 ) (−e^(−z) )dz =∫_(−∞) ^(+∞) e^(−(z^2 +z)) dz=∫_(−∞) ^(+∞) e^(−(z^2 +z+(1/4)−(1/4))) dz =e^(1/4) ∫_(−∞) ^(+∞) e^(−(z+(1/2))^2 ) dz (z+(1/2)=u) =e^(1/4) ∫_(−∞) ^(+∞) e^(−u^2 ) du=(√π)×e^(1/4)

$${I}=\int_{\mathrm{0}} ^{\infty} \:{e}^{{lnx}.{ln}\left(\frac{\mathrm{1}}{{x}}\right)} {dx}=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({lnx}\right)^{\mathrm{2}} } \:{dx} \\ $$$${we}\:{do}\:{the}\:{changement}\:{lnx}=−{z}\:\Rightarrow{x}={e}^{−{z}} \\ $$$${and}\:{I}=\int_{\infty} ^{−\infty} {e}^{−{z}^{\mathrm{2}} } \left(−{e}^{−{z}} \right){dz} \\ $$$$=\int_{−\infty} ^{+\infty} \:{e}^{−\left({z}^{\mathrm{2}} +{z}\right)} {dz}=\int_{−\infty} ^{+\infty} {e}^{−\left({z}^{\mathrm{2}} +{z}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right)} {dz} \\ $$$$={e}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\int_{−\infty} ^{+\infty} \:{e}^{−\left({z}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } {dz}\:\:\:\:\:\:\:\:\:\:\:\:\left({z}+\frac{\mathrm{1}}{\mathrm{2}}={u}\right) \\ $$$$={e}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\int_{−\infty} ^{+\infty} {e}^{−{u}^{\mathrm{2}} } {du}=\sqrt{\pi}×{e}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com