
Question Number 125276 by Study last updated on 09/Dec/20
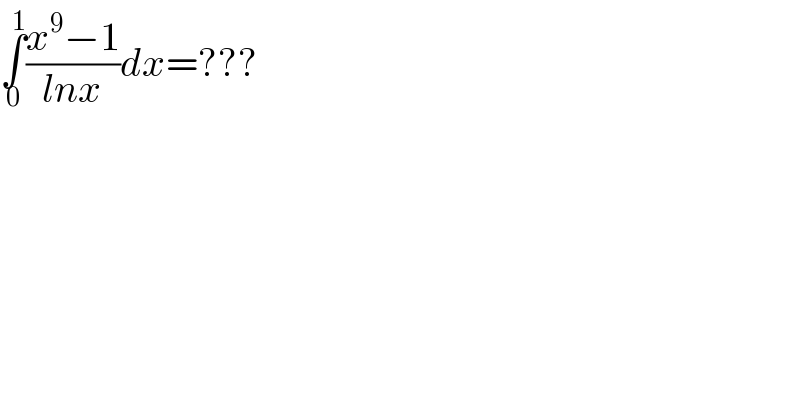
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{x}^{\mathrm{9}} −\mathrm{1}}{{lnx}}{dx}=??? \\ $$
Answered by Dwaipayan Shikari last updated on 09/Dec/20
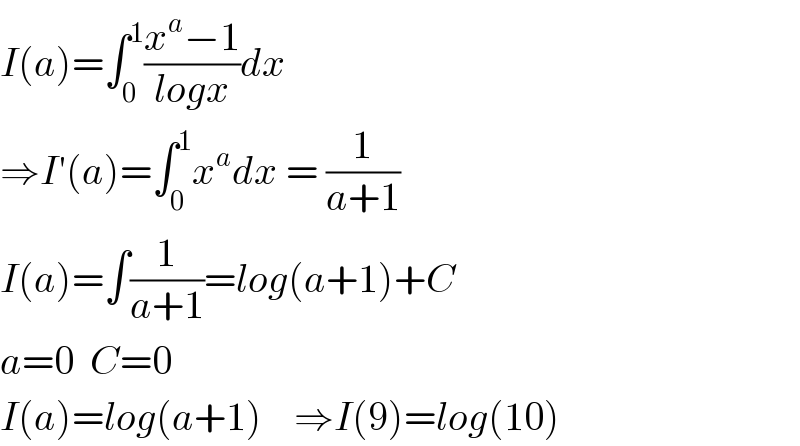
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{logx}}{dx} \\ $$$$\Rightarrow{I}'\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} {dx}\:=\:\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$${I}\left({a}\right)=\int\frac{\mathrm{1}}{{a}+\mathrm{1}}={log}\left({a}+\mathrm{1}\right)+{C}\:\:\:\:\: \\ $$$${a}=\mathrm{0}\:\:{C}=\mathrm{0} \\ $$$${I}\left({a}\right)={log}\left({a}+\mathrm{1}\right)\:\:\:\:\Rightarrow{I}\left(\mathrm{9}\right)={log}\left(\mathrm{10}\right) \\ $$
Answered by mathmax by abdo last updated on 09/Dec/20
![I=∫_0 ^1 ((x^9 −1)/(lnx))dx changement lnx=−t give x=e^(−t) I =−∫_0 ^∞ ((e^(−9t) −1)/(−t))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−10t) −e^(−t) )/t)dt =∫_0 ^∞ ((e^(−t) −e^(−10t) )/t)dt let f(x) =∫_0 ^∞ ((e^(−t) −e^(−10t) )/t)e^(−xt) dt with[x>0 f^′ (x)=−∫_0 ^∞ (e^(−t) −e^(−10t) )e^(−xt) dt =∫_0 ^∞ (e^(−(x+10)t) −e^(−(x+1)t) )dt =[−(1/(x+10))e^(−(x+10)t) +(1/(x+1))e^(−(x+1)t) ]_0 ^∞ =(1/(x+10))−(1/(x+1)) ⇒f(x)=ln(((x+10)/(x+1)))+C due to continuity ∃m >0 /∣f(x)∣≤m∫_0 ^∞ e^(−xt) dt =(m/x)→0 (x→+∞) ⇒c=0 ⇒ f(x)=ln(((x+10)/(x+1))) and I =f(0) =ln(10)](Q125299.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{9}} −\mathrm{1}}{\mathrm{lnx}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}=−\mathrm{t}\:\mathrm{give}\:\:\mathrm{x}=\mathrm{e}^{−\mathrm{t}} \\ $$$$\mathrm{I}\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{9t}} −\mathrm{1}}{−\mathrm{t}}\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt}\:=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{10t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} −\mathrm{e}^{−\mathrm{10t}} }{\mathrm{t}}\mathrm{dt}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} −\mathrm{e}^{−\mathrm{10t}} }{\mathrm{t}}\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:\:\mathrm{with}\left[\mathrm{x}>\mathrm{0}\right. \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=−\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{e}^{−\mathrm{t}} −\mathrm{e}^{−\mathrm{10t}} \right)\mathrm{e}^{−\mathrm{xt}} \mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{e}^{−\left(\mathrm{x}+\mathrm{10}\right)\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right)\mathrm{dt} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{10}}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{10}\right)\mathrm{t}} +\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\left(\frac{\mathrm{x}+\mathrm{10}}{\mathrm{x}+\mathrm{1}}\right)+\mathrm{C}\:\:\mathrm{due}\:\mathrm{to}\:\mathrm{continuity} \\ $$$$\exists\mathrm{m}\:\:>\mathrm{0}\:\:\:/\mid\mathrm{f}\left(\mathrm{x}\right)\mid\leqslant\mathrm{m}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{xt}} \mathrm{dt}\:=\frac{\mathrm{m}}{\mathrm{x}}\rightarrow\mathrm{0}\:\left(\mathrm{x}\rightarrow+\infty\right)\:\Rightarrow\mathrm{c}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\left(\frac{\mathrm{x}+\mathrm{10}}{\mathrm{x}+\mathrm{1}}\right)\:\:\mathrm{and}\:\mathrm{I}\:=\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{ln}\left(\mathrm{10}\right) \\ $$
