
Question Number 155619 by mathdanisur last updated on 02/Oct/21
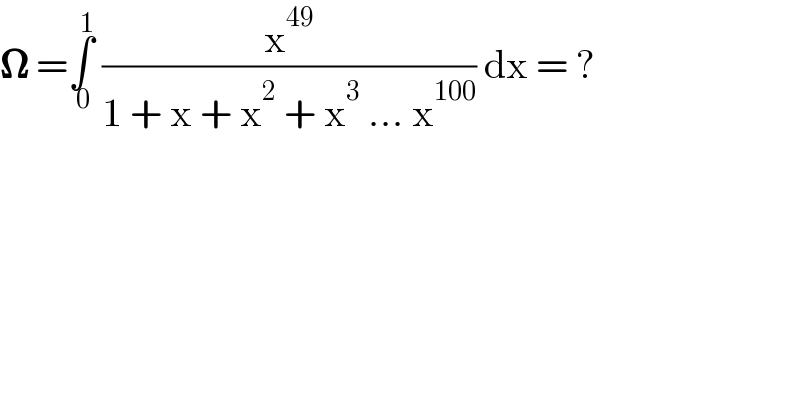
$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{\mathrm{x}^{\mathrm{49}} }{\mathrm{1}\:+\:\mathrm{x}\:+\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}^{\mathrm{3}} \:...\:\mathrm{x}^{\mathrm{100}} }\:\mathrm{dx}\:=\:? \\ $$
Answered by mindispower last updated on 04/Oct/21
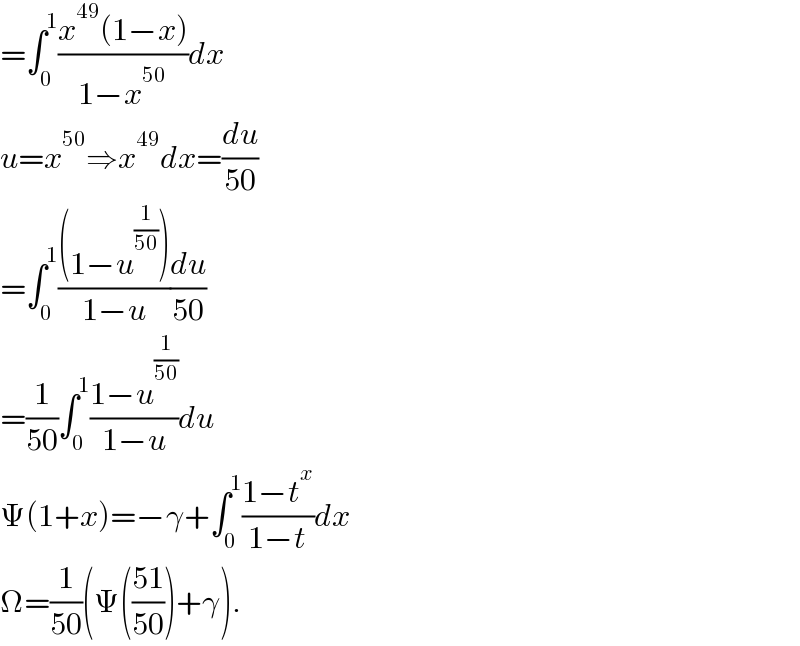
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{49}} \left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}^{\mathrm{50}} }{dx} \\ $$$${u}={x}^{\mathrm{50}} \Rightarrow{x}^{\mathrm{49}} {dx}=\frac{{du}}{\mathrm{50}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{u}^{\frac{\mathrm{1}}{\mathrm{50}}} \right)}{\mathrm{1}−{u}}\frac{{du}}{\mathrm{50}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{50}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{u}^{\frac{\mathrm{1}}{\mathrm{50}}} }{\mathrm{1}−{u}}{du} \\ $$$$\Psi\left(\mathrm{1}+{x}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{{x}} }{\mathrm{1}−{t}}{dx} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{50}}\left(\Psi\left(\frac{\mathrm{51}}{\mathrm{50}}\right)+\gamma\right). \\ $$
Commented by puissant last updated on 04/Oct/21
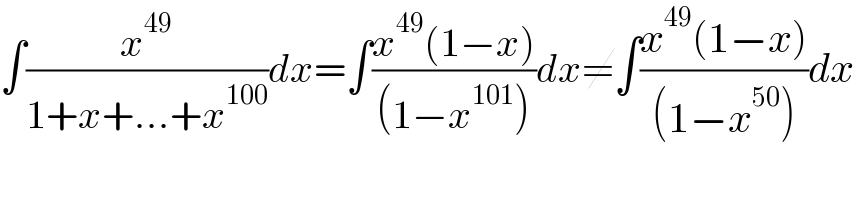
$$\int\frac{{x}^{\mathrm{49}} }{\mathrm{1}+{x}+...+{x}^{\mathrm{100}} }{dx}=\int\frac{{x}^{\mathrm{49}} \left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}^{\mathrm{101}} \right)}{dx}\neq\int\frac{{x}^{\mathrm{49}} \left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}^{\mathrm{50}} \right)}{dx} \\ $$
Commented by mindispower last updated on 04/Oct/21
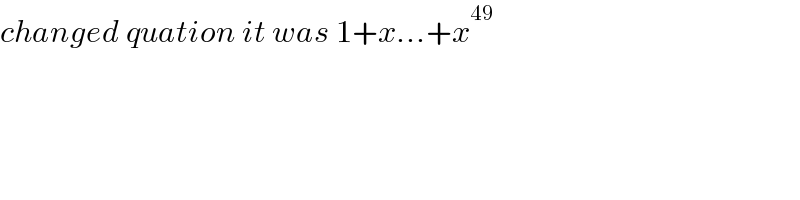
$${changed}\:{quation}\:{it}\:{was}\:\mathrm{1}+{x}...+{x}^{\mathrm{49}} \\ $$
Commented by puissant last updated on 04/Oct/21
����
