
Question Number 211400 by Spillover last updated on 08/Sep/24
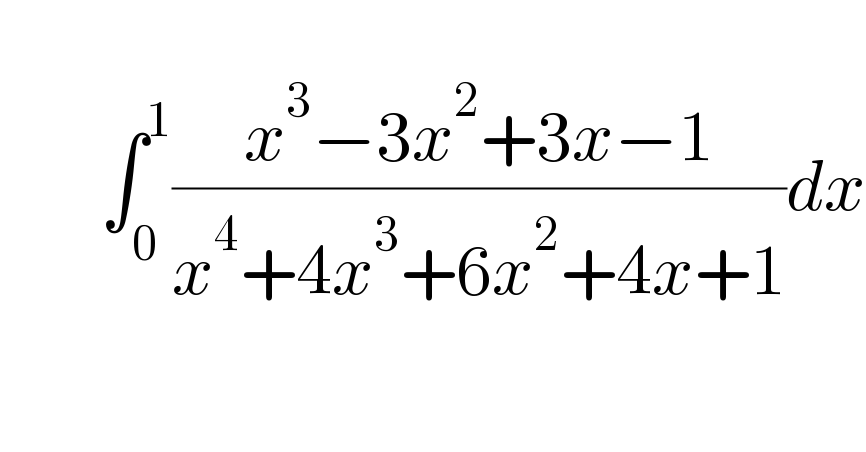
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}}{dx} \\ $$$$ \\ $$
Answered by Berbere last updated on 08/Sep/24
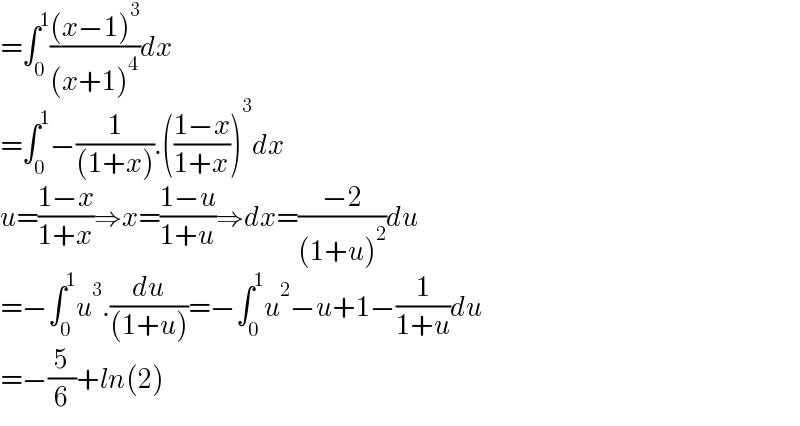
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }{\left({x}+\mathrm{1}\right)^{\mathrm{4}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)}.\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{3}} {dx} \\ $$$${u}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\Rightarrow{x}=\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\Rightarrow{dx}=\frac{−\mathrm{2}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{3}} .\frac{{du}}{\left(\mathrm{1}+{u}\right)}=−\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{2}} −{u}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{u}}{du} \\ $$$$=−\frac{\mathrm{5}}{\mathrm{6}}+{ln}\left(\mathrm{2}\right) \\ $$
Answered by Frix last updated on 08/Sep/24
![∫_0 ^1 (((x−1)^3 )/((x+1)^4 ))dx =^(t=x+1) =∫_1 ^2 ((1/t)−(6/t^2 )+((12)/t^3 )−(8/t^4 ))dt= =[ln t +(6/t)−(6/t^2 )+(8/(3t^3 ))]_1 ^2 =−(5/6)+ln 2](Q211409.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }{\left({x}+\mathrm{1}\right)^{\mathrm{4}} }{dx}\:\overset{{t}={x}+\mathrm{1}} {=} \\ $$$$=\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{6}}{{t}^{\mathrm{2}} }+\frac{\mathrm{12}}{{t}^{\mathrm{3}} }−\frac{\mathrm{8}}{{t}^{\mathrm{4}} }\right){dt}= \\ $$$$=\left[\mathrm{ln}\:{t}\:+\frac{\mathrm{6}}{{t}}−\frac{\mathrm{6}}{{t}^{\mathrm{2}} }+\frac{\mathrm{8}}{\mathrm{3}{t}^{\mathrm{3}} }\right]_{\mathrm{1}} ^{\mathrm{2}} =−\frac{\mathrm{5}}{\mathrm{6}}+\mathrm{ln}\:\mathrm{2} \\ $$
Answered by MathematicalUser2357 last updated on 10/Sep/24

$$−\mathrm{0}.\mathrm{140186} \\ $$
