
Question Number 127543 by Ar Brandon last updated on 30/Dec/20

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2021}} }{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Dec/20
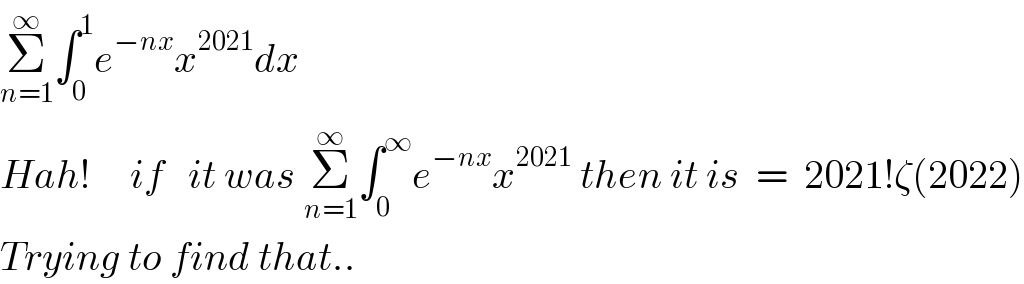
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{nx}} {x}^{\mathrm{2021}} {dx}\: \\ $$$${Hah}!\:\:\:\:\:{if}\:\:\:{it}\:{was}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {e}^{−{nx}} {x}^{\mathrm{2021}} \:{then}\:{it}\:{is}\:\:=\:\:\mathrm{2021}!\zeta\left(\mathrm{2022}\right) \\ $$$${Trying}\:{to}\:{find}\:{that}.. \\ $$
Commented by Ar Brandon last updated on 30/Dec/20

$$ \\ $$😃
Answered by mindispower last updated on 31/Dec/20
![=∫_0 ^1 (x/(e^x −1))=∫_0 ^∞ (x/(e^x −1))dx−∫_1 ^∞ ((xe^(−x) )/(1−e^(−x) ))dx ⇒=Γ(2)ζ(2)+[ln(1−e^(−x) )]_1 ^∞ +∫_1 ^∞ ln(1−e^(−x) )dx =ζ(2)ζ(2)+ln(1−e^(−1) )+∫_e^− ^0 ((ln(1−t))/t)dt =ζ(2)Γ(2)+ln(1−e^(−1) )−Li_2 ((1/e)) iwillfinish later ∫_0 ^1 (x^n /(e^x +1))dx =ζ(n+1)Γ(n+1)+Σ_(k=1) ^(n+1) a_k Li_k (b_k ) Li_1 (x)=ln(1−t)... i think not sur that in this forme](Q127613.png)
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{{e}^{{x}} −\mathrm{1}}=\int_{\mathrm{0}} ^{\infty} \frac{{x}}{{e}^{{x}} −\mathrm{1}}{dx}−\int_{\mathrm{1}} ^{\infty} \frac{{xe}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }{dx} \\ $$$$\Rightarrow=\Gamma\left(\mathrm{2}\right)\zeta\left(\mathrm{2}\right)+\left[{ln}\left(\mathrm{1}−{e}^{−{x}} \right)\right]_{\mathrm{1}} ^{\infty} +\int_{\mathrm{1}} ^{\infty} {ln}\left(\mathrm{1}−{e}^{−{x}} \right){dx} \\ $$$$=\zeta\left(\mathrm{2}\right)\zeta\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)+\int_{{e}^{−} } ^{\mathrm{0}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$=\zeta\left(\mathrm{2}\right)\Gamma\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}−{e}^{−\mathrm{1}} \right)−{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{e}}\right) \\ $$$${iwillfinish}\:{later}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{{e}^{{x}} +\mathrm{1}}{dx} \\ $$$$=\zeta\left({n}+\mathrm{1}\right)\Gamma\left({n}+\mathrm{1}\right)+\underset{{k}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}{a}_{{k}} {Li}_{{k}} \left({b}_{{k}} \right)\: \\ $$$${Li}_{\mathrm{1}} \left({x}\right)={ln}\left(\mathrm{1}−{t}\right)... \\ $$$${i}\:{think}\:{not}\:{sur}\:{that}\:{in}\:{this}\:{forme} \\ $$
