
Question Number 542 by 123456 last updated on 25/Jan/15
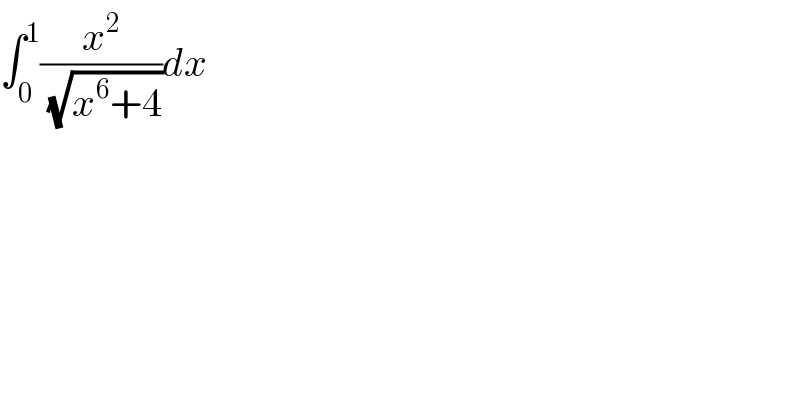
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\sqrt{{x}^{\mathrm{6}} +\mathrm{4}}}{dx} \\ $$
Answered by prakash jain last updated on 24/Jan/15
![x^3 =u x^2 dx=(du/3) x=0, u=0 x=1, u=1 ∫_0 ^1 (x^2 /(√(x^6 +4)))dx=∫_0 ^1 (1/3)∙(1/(√(u^2 +2^2 )))du =[(1/3)ln (u+(√(u^2 +4)))]_0 ^1 =(1/3)[ln (1+(√5))−ln 2] =(1/3)ln ((1+(√5))/2)](Q547.png)
$${x}^{\mathrm{3}} ={u} \\ $$$${x}^{\mathrm{2}} {dx}=\frac{{du}}{\mathrm{3}} \\ $$$${x}=\mathrm{0},\:{u}=\mathrm{0} \\ $$$${x}=\mathrm{1},\:{u}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\sqrt{{x}^{\mathrm{6}} +\mathrm{4}}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\sqrt{{u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}{du} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left({u}+\sqrt{{u}^{\mathrm{2}} +\mathrm{4}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)−\mathrm{ln}\:\mathrm{2}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
