Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 160577 by mnjuly1970 last updated on 02/Dec/21

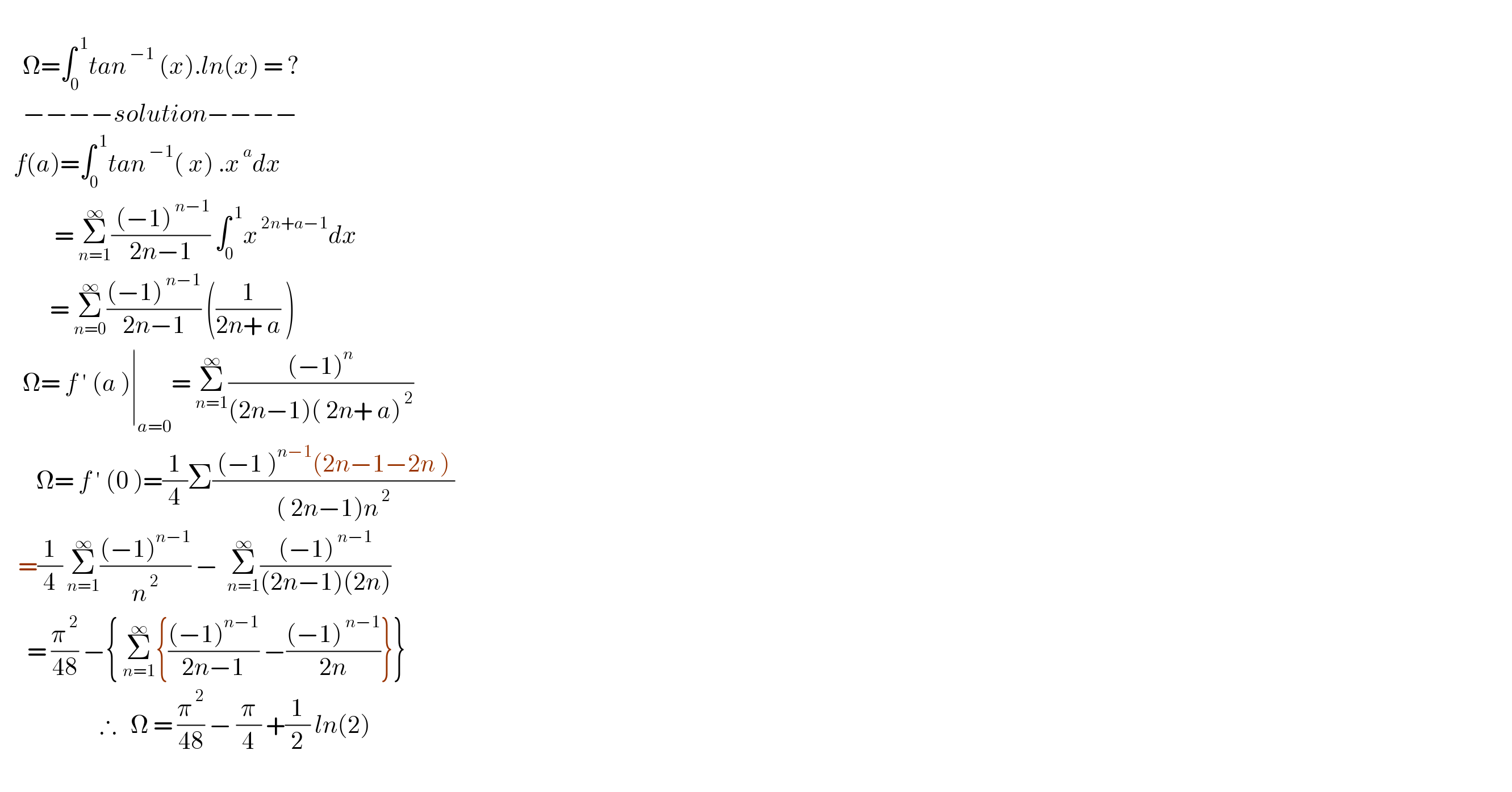
Ω=∫_0 ^( 1) tan^( −1) (x).ln(x) = ? −−−−solution−−−− f(a)=∫_0 ^( 1) tan^( −1) ( x) .x^( a) dx = Σ_(n=1) ^∞ (( (−1)^( n−1) )/(2n−1)) ∫_0 ^( 1) x^( 2n+a−1) dx = Σ_(n=0) ^∞ (((−1)^( n−1) )/(2n−1)) ((1/(2n+ a)) ) Ω= f ′ (a )∣_(a=0) = Σ_(n=1) ^∞ (((−1)^n )/((2n−1)( 2n+ a)^( 2) )) Ω= f ′ (0 )=(1/4)Σ(( (−1 )^(n−1) (2n−1−2n ) )/(( 2n−1)n^( 2) )) =(1/4) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^( 2) ) − Σ_(n=1) ^∞ (((−1)^( n−1) )/((2n−1)(2n))) = (π^( 2) /(48)) −{ Σ_(n=1) ^∞ {(((−1)^(n−1) )/(2n−1)) −(((−1)^( n−1) )/(2n))}} ∴ Ω = (π^( 2) /(48)) − (π/4) +(1/2) ln(2)

$$ \\ $$$$\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} {tan}^{\:−\mathrm{1}} \:\left({x}\right).{ln}\left({x}\right)\:=\:? \\ $$$$\:\:\:\:\:−−−−{solution}−−−− \\ $$$$\:\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} {tan}^{\:−\mathrm{1}} \left(\:{x}\right)\:.{x}^{\:{a}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\:\mathrm{2}{n}+{a}−\mathrm{1}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}}\:\left(\frac{\mathrm{1}}{\mathrm{2}{n}+\:{a}}\:\right) \\ $$$$\:\:\:\:\:\Omega=\:{f}\:'\:\left({a}\:\right)\mid_{{a}=\mathrm{0}} =\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\:\mathrm{2}{n}+\:{a}\right)^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\Omega=\:{f}\:'\:\left(\mathrm{0}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}\Sigma\frac{\:\left(−\mathrm{1}\:\right)^{{n}−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{1}−\mathrm{2}{n}\:\right)\:}{\left(\:\mathrm{2}{n}−\mathrm{1}\right){n}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\:\mathrm{2}} }\:−\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}\right)} \\ $$$$\:\:\:\:\:\:=\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{48}}\:−\left\{\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}}\:−\frac{\left(−\mathrm{1}\right)^{\:{n}−\mathrm{1}} }{\mathrm{2}{n}}\right\}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\Omega\:=\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{48}}\:−\:\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$

Answered by Kamel last updated on 03/Dec/21

Integration by part: Ω=[(xLn(x)−x)Arctan(x)]_0 ^1 −∫_0 ^1 ((xLn(x)−x)/(1+x^2 ))dx =^(t=x^2 ) −(π/4)−(1/4)∫_0 ^1 ((Ln(t))/(1+t))dt_(=^(IBP) −∫_0 ^1 ((Ln(1+t))/t)dt=−(π^2 /(12))) +(1/2)Ln(2) =(π^2 /(48))−(π/4)+(1/2)Ln(2)

$${Integration}\:{by}\:{part}: \\ $$$$\Omega=\left[\left({xLn}\left({x}\right)−{x}\right){Arctan}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xLn}\left({x}\right)−{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\overset{{t}={x}^{\mathrm{2}} } {=}−\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\underset{\overset{{IBP}} {=}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left(\mathrm{1}+{t}\right)}{{t}}{dt}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}} {\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left({t}\right)}{\mathrm{1}+{t}}{dt}}+\frac{\mathrm{1}}{\mathrm{2}}{Ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:=\frac{\pi^{\mathrm{2}} }{\mathrm{48}}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{Ln}\left(\mathrm{2}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com