
Question Number 137141 by Ar Brandon last updated on 30/Mar/21
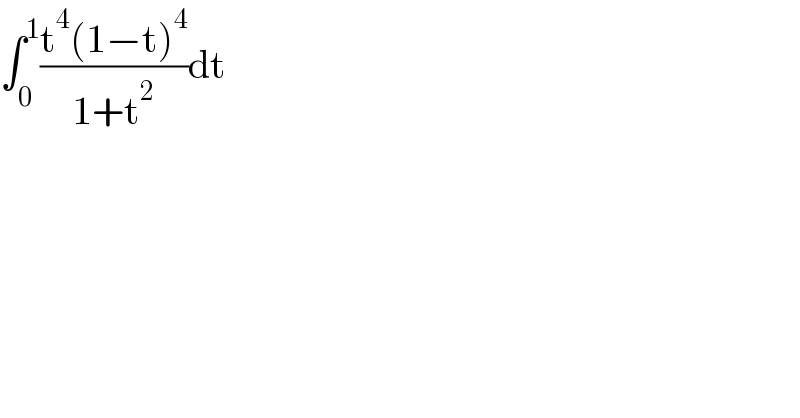
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{4}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$
Answered by Ar Brandon last updated on 30/Mar/21
![J=∫_0 ^1 ((t^4 (1−t)^4 )/(1+t^2 ))dt=∫_0 ^1 ((t^4 (1−4t+6t^2 −4t^3 +t^4 ))/(1+t^2 ))dt =∫_0 ^1 ((t^4 (1−4t+6t^2 −4t^3 +t^4 )(1−t^2 ))/(1−t^4 ))dt =^(u=t^4 ) (1/4)∫_0 ^1 ((u^(1/4) (1−4u^(1/4) +6u^(1/2) −4u^(3/4) +u)(1−u^(1/2) ))/(1−u))du =(1/4){[ψ((7/4))−ψ((5/4))]−4[ψ(2)−ψ((3/2))]+6[ψ((9/4))−ψ((7/4))] {−4[ψ((5/2))−ψ(2)]+[ψ(((11)/4))−ψ((9/4))]} =(1/4){[(4/3)+ψ((3/4))−4−ψ((1/4))]−4[1+ψ(1)−2−ψ((1/2))] {+6[(4/5)+4+ψ((1/4))−(4/3)−ψ((3/4))] {−4[(2/3)+2+ψ((1/2))−1−ψ(1)]+[(4/7)+(4/3)+ψ((3/4))−(4/5)−4−ψ((1/4))]} =(1/4){[−(8/3)+π]−4[−1+2ln2]+6[((52)/(15))−π]−4[(5/3)−2ln2]+[−((304)/(105))+π]} =(1/4){((88)/7)−4π}=((22)/7)−𝛑](Q137142.png)
$$\mathrm{J}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{4}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{4t}+\mathrm{6t}^{\mathrm{2}} −\mathrm{4t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{4}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{4t}+\mathrm{6t}^{\mathrm{2}} −\mathrm{4t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{4}} \right)\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$$$\:\:\overset{\mathrm{u}=\mathrm{t}^{\mathrm{4}} } {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{1}−\mathrm{4u}^{\frac{\mathrm{1}}{\mathrm{4}}} +\mathrm{6u}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{4u}^{\frac{\mathrm{3}}{\mathrm{4}}} +\mathrm{u}\right)\left(\mathrm{1}−\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)}{\mathrm{1}−\mathrm{u}}\mathrm{du} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left[\psi\left(\frac{\mathrm{7}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\right]−\mathrm{4}\left[\psi\left(\mathrm{2}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right]+\mathrm{6}\left[\psi\left(\frac{\mathrm{9}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{7}}{\mathrm{4}}\right)\right]\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left\{−\mathrm{4}\left[\psi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)−\psi\left(\mathrm{2}\right)\right]+\left[\psi\left(\frac{\mathrm{11}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{9}}{\mathrm{4}}\right)\right]\right\} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left[\frac{\mathrm{4}}{\mathrm{3}}+\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\mathrm{4}−\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right]−\mathrm{4}\left[\mathrm{1}+\psi\left(\mathrm{1}\right)−\mathrm{2}−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right]\right. \\ $$$$\:\:\:\:\:\:\left\{+\mathrm{6}\left[\frac{\mathrm{4}}{\mathrm{5}}+\mathrm{4}+\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\frac{\mathrm{4}}{\mathrm{3}}−\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right]\right. \\ $$$$\:\:\:\:\:\:\left\{−\mathrm{4}\left[\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}+\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}−\psi\left(\mathrm{1}\right)\right]+\left[\frac{\mathrm{4}}{\mathrm{7}}+\frac{\mathrm{4}}{\mathrm{3}}+\psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\frac{\mathrm{4}}{\mathrm{5}}−\mathrm{4}−\psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right]\right\} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left[−\frac{\mathrm{8}}{\mathrm{3}}+\pi\right]−\mathrm{4}\left[−\mathrm{1}+\mathrm{2ln2}\right]+\mathrm{6}\left[\frac{\mathrm{52}}{\mathrm{15}}−\pi\right]−\mathrm{4}\left[\frac{\mathrm{5}}{\mathrm{3}}−\mathrm{2ln2}\right]+\left[−\frac{\mathrm{304}}{\mathrm{105}}+\pi\right]\right\} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\mathrm{88}}{\mathrm{7}}−\mathrm{4}\pi\right\}=\frac{\mathrm{22}}{\mathrm{7}}−\boldsymbol{\pi} \\ $$
Commented by Ar Brandon last updated on 30/Mar/21
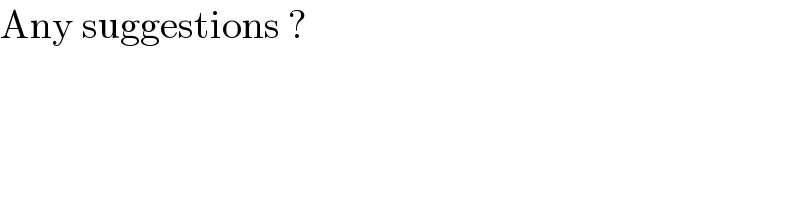
$$\mathrm{Any}\:\mathrm{suggestions}\:? \\ $$
Commented by mnjuly1970 last updated on 30/Mar/21
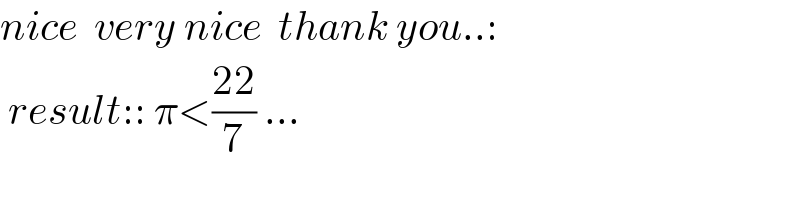
$${nice}\:\:{very}\:{nice}\:\:{thank}\:{you}..: \\ $$$$\:{result}::\:\pi<\frac{\mathrm{22}}{\mathrm{7}}\:... \\ $$
Commented by Ar Brandon last updated on 30/Mar/21
Thanks for your approuval, Sir
Answered by Dwaipayan Shikari last updated on 30/Mar/21

Commented by Ar Brandon last updated on 30/Mar/21

$$\mathrm{Nice}\:\mathrm{decomposition}\:!\:\mathrm{Thanks} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Mar/21

$$ \\ $$😃
Commented by mnjuly1970 last updated on 30/Mar/21
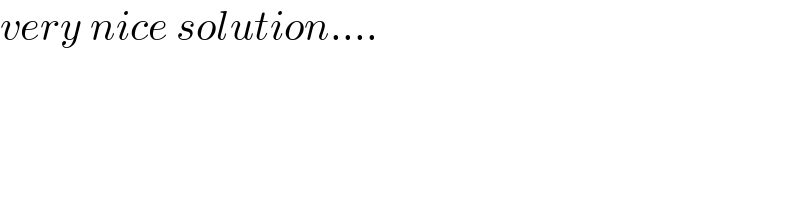
$${very}\:{nice}\:{solution}.... \\ $$
