
Question Number 216615 by EmGent last updated on 12/Feb/25
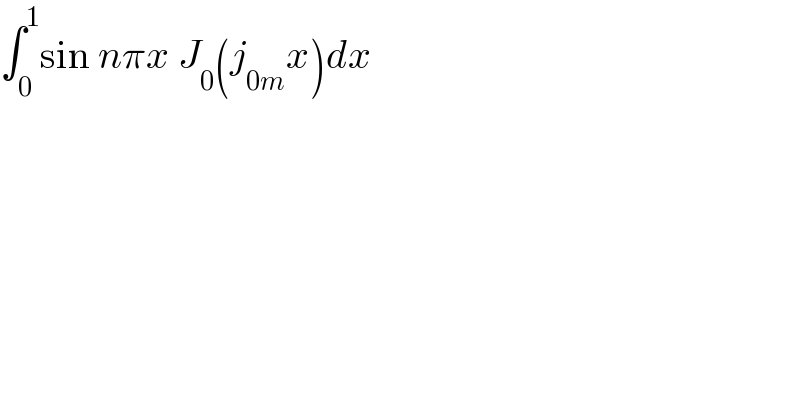
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}\:{n}\pi{x}\:{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx} \\ $$
Answered by EmGent last updated on 12/Feb/25
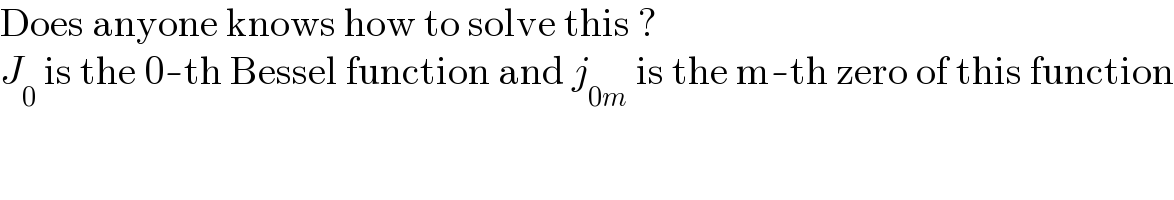
$$\mathrm{Does}\:\mathrm{anyone}\:\mathrm{knows}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:? \\ $$$${J}_{\mathrm{0}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{0}-\mathrm{th}\:\mathrm{Bessel}\:\mathrm{function}\:\mathrm{and}\:{j}_{\mathrm{0}{m}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{m}-\mathrm{th}\:\mathrm{zero}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function} \\ $$
Answered by MrGaster last updated on 13/Feb/25
![I=∫_0 ^1 sin nπx J_0 (j_(0m) x)dx ∫_0 ^1 x J_0 (j_(0m) x)J_0 (j_(0m) x)dx=(1/2)[J_1 (j_(0m) )]^2 δ_(mn) whene δ_(mn) is the Kronecker delta. sin n πx=((e^(inπx) −e^(−inπx) )/(2i)) I=∫_0 ^1 ((e^(inπx) −e^(iπnx) )/(2i))J_0 (j_(0m) x)dx =(1/(2i))(∫_0 ^1 e^(inπx) J_0 (j_(0m) x)dx−∫_0 ^1 e^(−inπx) J_0 (j_(0m) x)dx) ∫_0 ^1 e^(ax) J_0 (j_(0m) x)dx=((e^a −J_0 (j_(0m) ))/(a^2 +j_(0m) ^2 )) For a=inπ,have: ∫_0 ^1 e^(inπx) J_0 (j_(0m) x)dx=((e^(inπ) −J_0 (j_(0m) ))/((inπ)^2 +j_(0m) ^2 )) ∫_0 ^1 e^(−inπx) J_0 (j_(0m) x)dx=((e^(−inπ) −J_0 (j_(0m) ))/((inπ)^2 +j_(0m) ^2 )) I=(1/(2i))(((e^(inx) −J_0 (j_(0m) ))/((inπ)^2 +j_(0m) ^2 ))−((e^(−inπ) −J_0 (j_(0m) ))/((−inπ)^2 +j_(0m) ^2 ))) =(1/(2i))(((e^(inπ) −e^(−inπ) )/((inπ)^2 +j_(0m) ^2 ))) =(1/(2i))(((2i sin nπ)/((inπ)^2 +j_(0m) ^2 ))) ⇒ determinant (((I=((2 sin(j_(0m) ))/(j_(0m) (1−(((nπ)/j_(0m) ))^2 ))))))](Q216635.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{sin}\:{n}\pi{x}\:{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}\:{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[{J}_{\mathrm{1}} \left({j}_{\mathrm{0}{m}} \right)\right]^{\mathrm{2}} \delta_{{mn}} \\ $$$$\mathrm{whene}\:\delta_{{mn}} \mathrm{is}\:\mathrm{the}\:\mathrm{Kronecker}\:\mathrm{delta}. \\ $$$$\mathrm{sin}\:{n}\:\pi{x}=\frac{{e}^{{in}\pi{x}} −{e}^{−{in}\pi{x}} }{\mathrm{2}{i}} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{{in}\pi{x}} −{e}^{{i}\pi{nx}} }{\mathrm{2}{i}}{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{in}\pi{x}} {J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx}−\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{in}\pi{x}} {J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{ax}} {J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx}=\frac{{e}^{{a}} −{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} \right)}{{a}^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} } \\ $$$$\mathrm{For}\:{a}={in}\pi,\mathrm{have}: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{in}\pi{x}} {J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx}=\frac{{e}^{{in}\pi} −{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} \right)}{\left({in}\pi\right)^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{in}\pi{x}} {J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} {x}\right){dx}=\frac{{e}^{−{in}\pi} −{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} \right)}{\left({in}\pi\right)^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} } \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\frac{{e}^{{inx}} −{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} \right)}{\left({in}\pi\right)^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} }−\frac{{e}^{−{in}\pi} −{J}_{\mathrm{0}} \left({j}_{\mathrm{0}{m}} \right)}{\left(−{in}\pi\right)^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\frac{{e}^{{in}\pi} −{e}^{−{in}\pi} }{\left({in}\pi\right)^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left(\frac{\mathrm{2}{i}\:\mathrm{sin}\:{n}\pi}{\left({in}\pi\right)^{\mathrm{2}} +{j}_{\mathrm{0}{m}} ^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\begin{array}{|c|}{{I}=\frac{\mathrm{2}\:\mathrm{sin}\left({j}_{\mathrm{0}{m}} \right)}{{j}_{\mathrm{0}{m}} \left(\mathrm{1}−\left(\frac{{n}\pi}{{j}_{\mathrm{0}{m}} }\right)^{\mathrm{2}} \right)}}\\\hline\end{array} \\ $$
Commented by EmGent last updated on 15/Sep/25

$$\mathrm{How}\:\mathrm{do}\:\mathrm{go}\:\mathrm{from}\:\mathrm{blue}\:\mathrm{to}\:\mathrm{the}\:\mathrm{red}, \\ $$$$\mathrm{also}\:\mathrm{shouldn}\:\mathrm{t}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{expression}\:\mathrm{always}\:\mathrm{be}\:\mathrm{0}\:? \\ $$
