
Question Number 217289 by Frix last updated on 08/Mar/25
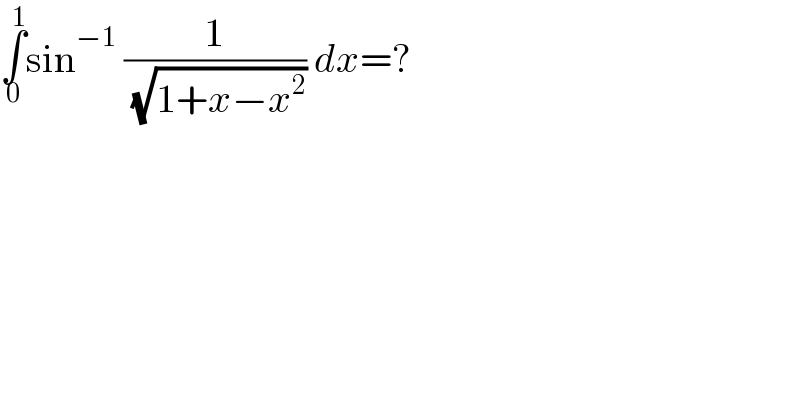
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}−{x}^{\mathrm{2}} }}\:{dx}=? \\ $$
Commented by Ghisom last updated on 11/Mar/25

$$\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{partial}\:\mathrm{integration} \\ $$$$\:\:\:\:\:{u}'=\mathrm{1}\wedge{v}=\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{1}}{\:\sqrt{−{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$\mathrm{but}\:\mathrm{then}\:\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{not}\:\mathrm{nice}... \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\frac{\pi}{\varphi^{\mathrm{2}} }=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\pi\:\mathrm{but}\:\mathrm{I}\:\mathrm{found}\:\mathrm{no} \\ $$$$\mathrm{way}\:\mathrm{to}\:\mathrm{clearly}\:\mathrm{get}\:\mathrm{it}\:\mathrm{yet} \\ $$
Answered by Ghisom last updated on 12/Mar/25
![I finally found a good path using Feynman′s trick: ∫_0 ^1 arcsin (1/( (√(−x^2 +x+1)))) dx= =2∫_0 ^(1/2) arctan (1/( (√x)(√(1−x)))) dx Ω(α)=2∫_0 ^(1/2) arctan (α/( (√x)(√(1−x)))) dx Ω′(α)=2∫_0 ^(1/2) (((√x)(√(1−x)))/(x(1−x)+α^2 ))dx= [t=arcsin (√x) → dx=2(√x)(√(1−x))dt] =4∫_0 ^(π/4) ((cos^2 t sin^2 t)/(α^2 +cos^2 t sin^2 t))dt= =4∫_0 ^(π/4) dt−4α^2 ∫_0 ^(π/4) (dt/(α^2 +cos^2 t sin^2 t))= [u=tan 2t → dt=(du/(2(u^2 +1)))] =π−((8α^2 )/(4α^2 +1))∫_0 ^∞ (du/(u^2 +((4α^2 )/(4α^2 +1))))= =π−((4α)/( (√(4α^2 +1))))[arctan (((√(4α^2 +1))u)/(2α))]_0 ^∞ = =π(1−((2α)/( (√(4α^2 +1)))))=Ω′(α) Ω(α)=π(∫dα−∫((2α)/( (√(4α^2 +1))))dα)= =π(α−((√(4α^2 +1))/2)+C) Ω(0)=0 ⇒ C=(1/2) Ω(α)=π(α−((√(4α^2 +1))/2)+(1/2)) Ω(1)=((3−(√5))/2)π=(π/ϕ^2 )](Q217390.png)
$$\mathrm{I}\:\mathrm{finally}\:\mathrm{found}\:\mathrm{a}\:\mathrm{good}\:\mathrm{path}\:\mathrm{using} \\ $$$$\mathrm{Feynman}'\mathrm{s}\:\mathrm{trick}: \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{arcsin}\:\frac{\mathrm{1}}{\:\sqrt{−{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\:{dx}= \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\mathrm{arctan}\:\frac{\mathrm{1}}{\:\sqrt{{x}}\sqrt{\mathrm{1}−{x}}}\:{dx} \\ $$$$ \\ $$$$\Omega\left(\alpha\right)=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\mathrm{arctan}\:\frac{\alpha}{\:\sqrt{{x}}\sqrt{\mathrm{1}−{x}}}\:{dx} \\ $$$$\Omega'\left(\alpha\right)=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\frac{\sqrt{{x}}\sqrt{\mathrm{1}−{x}}}{{x}\left(\mathrm{1}−{x}\right)+\alpha^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}\sqrt{\mathrm{1}−{x}}{dt}\right] \\ $$$$=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\mathrm{cos}^{\mathrm{2}} \:{t}\:\mathrm{sin}^{\mathrm{2}} \:{t}}{\alpha^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:{t}\:\mathrm{sin}^{\mathrm{2}} \:{t}}{dt}= \\ $$$$=\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{dt}−\mathrm{4}\alpha^{\mathrm{2}} \underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{{dt}}{\alpha^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:{t}\:\mathrm{sin}^{\mathrm{2}} \:{t}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{tan}\:\mathrm{2}{t}\:\rightarrow\:{dt}=\frac{{du}}{\mathrm{2}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}\right] \\ $$$$=\pi−\frac{\mathrm{8}\alpha^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{du}}{{u}^{\mathrm{2}} +\frac{\mathrm{4}\alpha^{\mathrm{2}} }{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$=\pi−\frac{\mathrm{4}\alpha}{\:\sqrt{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}}\left[\mathrm{arctan}\:\frac{\sqrt{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}{u}}{\mathrm{2}\alpha}\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\pi\left(\mathrm{1}−\frac{\mathrm{2}\alpha}{\:\sqrt{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}}\right)=\Omega'\left(\alpha\right) \\ $$$$\Omega\left(\alpha\right)=\pi\left(\int{d}\alpha−\int\frac{\mathrm{2}\alpha}{\:\sqrt{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}}{d}\alpha\right)= \\ $$$$=\pi\left(\alpha−\frac{\sqrt{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}}+{C}\right) \\ $$$$\Omega\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\:{C}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Omega\left(\alpha\right)=\pi\left(\alpha−\frac{\sqrt{\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Omega\left(\mathrm{1}\right)=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\pi=\frac{\pi}{\varphi^{\mathrm{2}} } \\ $$
Commented by Frix last updated on 12/Mar/25
��
