
Question Number 113190 by Dwaipayan Shikari last updated on 11/Sep/20
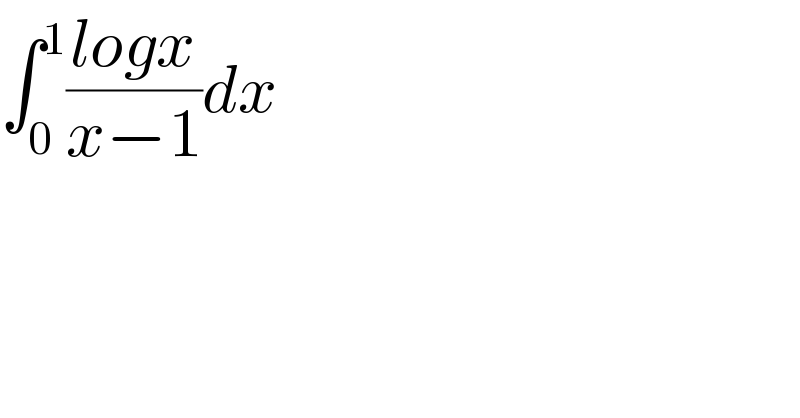
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}−\mathrm{1}}{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Sep/20
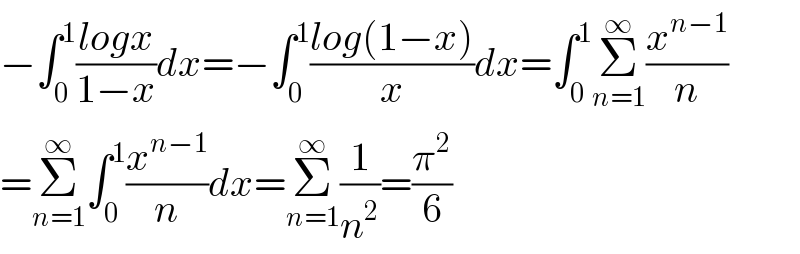
$$−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{\mathrm{1}−{x}}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}\right)}{{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}−\mathrm{1}} }{{n}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}−\mathrm{1}} }{{n}}{dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Sep/20

$${Is}\:{it}\:{right}? \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by mathdave last updated on 12/Sep/20
![solution let I=−∫_0 ^1 ((lnx)/(1−x))dx=−∫_0 ^1 Σ_(k=0) ^∞ x^k lnxdx (∂/∂a)∣_(a=1) I(a)=−Σ_(k=0) ^∞ (∂/∂a)∫_0 ^1 x^k .x^(a−1) dx=−Σ_(k=0) ^∞ (∂/∂a)∫_0 ^1 x^(k+a−1) dx I(a)=−Σ_(k=0) ^∞ (∂/∂a)[(1/(k+a))] I(1)=Σ_(k=0) ^∞ (1/((k+1)^2 ))=Σ_(k=1) ^∞ (1/k^2 )=(π^2 /6) ∵∫_0 ^1 ((lnx)/(x−1))dx=(π^2 /6)](Q113220.png)
$${solution}\: \\ $$$${let}\:{I}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{\mathrm{1}−{x}}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{k}} \mathrm{ln}{xdx} \\ $$$$\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} {I}\left({a}\right)=−\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} .{x}^{{a}−\mathrm{1}} {dx}=−\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}+{a}−\mathrm{1}} {dx} \\ $$$${I}\left({a}\right)=−\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\left[\frac{\mathrm{1}}{{k}+{a}}\right] \\ $$$${I}\left(\mathrm{1}\right)=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\because\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{{x}−\mathrm{1}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$
