Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 132191 by rs4089 last updated on 12/Feb/21

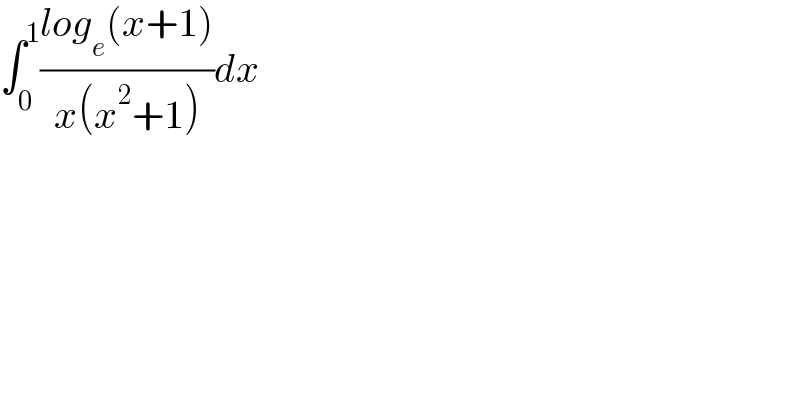
∫_0 ^1 ((log_e (x+1))/(x(x^2 +1)))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}_{{e}} \left({x}+\mathrm{1}\right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$

Answered by mathmax by abdo last updated on 12/Feb/21

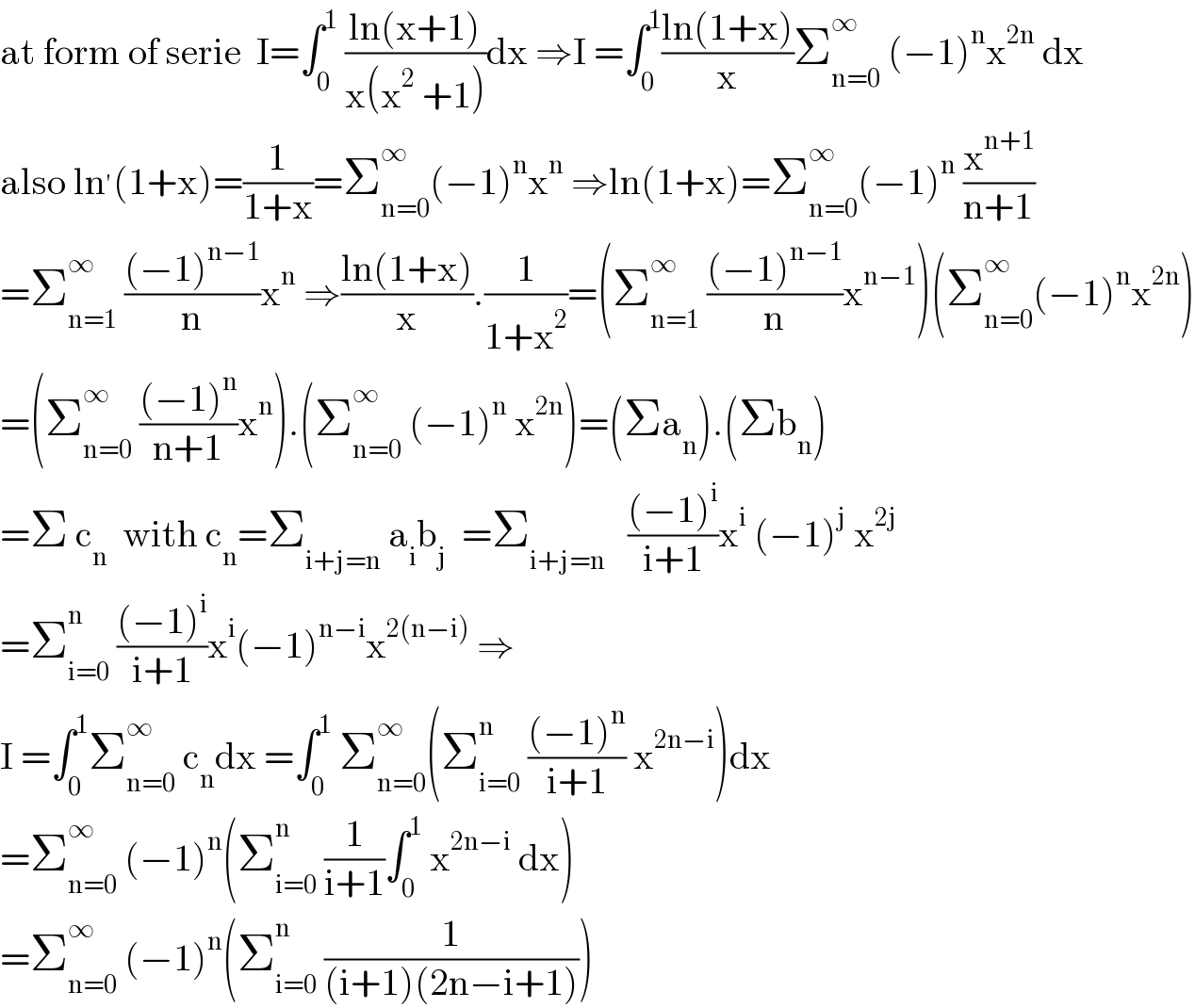
at form of serie I=∫_0 ^1 ((ln(x+1))/(x(x^2 +1)))dx ⇒I =∫_0 ^1 ((ln(1+x))/x)Σ_(n=0) ^∞ (−1)^n x^(2n) dx also ln^′ (1+x)=(1/(1+x))=Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (−1)^n (x^(n+1) /(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n ⇒((ln(1+x))/x).(1/(1+x^2 ))=(Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^(n−1) )(Σ_(n=0) ^∞ (−1)^n x^(2n) ) =(Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^n ).(Σ_(n=0) ^∞ (−1)^n x^(2n) )=(Σa_n ).(Σb_n ) =Σ c_n with c_n =Σ_(i+j=n) a_i b_j =Σ_(i+j=n) (((−1)^i )/(i+1))x^i (−1)^j x^(2j) =Σ_(i=0) ^n (((−1)^i )/(i+1))x^i (−1)^(n−i) x^(2(n−i)) ⇒ I =∫_0 ^1 Σ_(n=0) ^∞ c_n dx =∫_0 ^1 Σ_(n=0) ^∞ (Σ_(i=0) ^n (((−1)^n )/(i+1)) x^(2n−i) )dx =Σ_(n=0) ^∞ (−1)^n (Σ_(i=0) ^n (1/(i+1))∫_0 ^1 x^(2n−i) dx) =Σ_(n=0) ^∞ (−1)^n (Σ_(i=0) ^n (1/((i+1)(2n−i+1))))

$$\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie}\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}} \:\mathrm{dx} \\ $$$$\mathrm{also}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{x}^{\mathrm{n}} \:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}.\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}} \right) \\ $$$$=\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}+\mathrm{1}}\mathrm{x}^{\mathrm{n}} \right).\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{2n}} \right)=\left(\Sigma\mathrm{a}_{\mathrm{n}} \right).\left(\Sigma\mathrm{b}_{\mathrm{n}} \right) \\ $$$$=\Sigma\:\mathrm{c}_{\mathrm{n}} \:\:\mathrm{with}\:\mathrm{c}_{\mathrm{n}} =\sum_{\mathrm{i}+\mathrm{j}=\mathrm{n}} \:\mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{j}} \:\:=\sum_{\mathrm{i}+\mathrm{j}=\mathrm{n}} \:\:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}+\mathrm{1}}\mathrm{x}^{\mathrm{i}} \:\left(−\mathrm{1}\right)^{\mathrm{j}} \:\mathrm{x}^{\mathrm{2j}} \\ $$$$=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{i}+\mathrm{1}}\mathrm{x}^{\mathrm{i}} \left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{i}} \mathrm{x}^{\mathrm{2}\left(\mathrm{n}−\mathrm{i}\right)} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{c}_{\mathrm{n}} \mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{i}+\mathrm{1}}\:\mathrm{x}^{\mathrm{2n}−\mathrm{i}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{i}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{i}} \:\mathrm{dx}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{i}+\mathrm{1}\right)\left(\mathrm{2n}−\mathrm{i}+\mathrm{1}\right)}\right) \\ $$

Answered by mathmax by abdo last updated on 12/Feb/21

let try parametric method Φ=∫_0 ^1 ((ln(1+x))/(x(x^2 +1)))dx let f(a)=∫_0 ^1 ((ln(1+ax))/(x(x^2 +1))) with a>0 ⇒f^′ (a)=∫_0 ^1 (x/((1+ax)x(x^2 +1)))dx =∫_0 ^1 (dx/((1+ax)(x^2 +1))) let decompose F(x)=(1/((ax+1)(x^2 +1))) F(x)=(α/(ax+1)) +((mx+n)/(x^2 +1)) α=(1/(((1/a^2 )+1)))=(a^2 /(1+a^2 )) ,lim_(x→+∞) xF(x)=0 =(α/a) +m ⇒m=−(α/a)=−(a/(1+a^2 )) F(0)=1 =α +n ⇒n=1−α =1−(a^2 /(1+a^2 ))=(1/(1+a^2 )) ⇒ F(x)=(a^2 /((1+a^2 )(ax+1))) +((−(a/(1+a^2 ))x+(1/(1+a^2 )))/(x^2 +1)) ⇒∫_0 ^1 F(x)dx =(a^2 /(1+a^2 ))∫_0 ^1 (dx/(ax+1))−(1/(1+a^2 ))∫_0 ^1 ((ax−1)/(x^2 +1))dx =(a/(1+a^2 ))[ln(ax+1)]_0 ^1 −(a/(2(1+a^2 )))[ln(1+x^2 )]_0 ^1 +(1/(1+a^2 )).(π/4) =(a/(1+a^2 ))ln(a+1)−((aln(2))/(2(1+a^2 )))+(π/(4(1+a^2 ))) ⇒ f(a) =∫ ((aln(a+1))/(1+a^2 ))da −((ln(2))/2)∫ ((ada)/(1+a^2 )) +(π/4) arctana +c =∫ ((aln(1+a))/(1+a^2 ))da−((ln(2))/4)ln(1+a^2 )+(π/4) arctan(a)+C ∫ (a/(a^2 +1))ln(1+a)da =(1/2)ln(a^2 +1)ln(1+a)−∫ (1/2)ln(a^2 +1)(da/(1+a)) =(1/2)ln(1+a)ln(1+a^2 )−(1/2)∫ ((ln(1+a^2 ))/(1+a))da ⇒ f(a)=∫_0 ^a ((xln(1+x))/(1+x^2 ))dx−((ln(2))/4)ln(1+a^2 )+(π/4) arctan(a) +C C=f(0)=0 f(1)=∫_0 ^1 ((xln(1+x))/(1+x^2 ))dx−((ln^2 (2))/4) +(π^2 /(16)) =Φ we have by parts ∫_0 ^1 ((xln(1+x))/(1+x^2 ))dx=[(1/2)ln(1+x)ln(1+x^2 )]_0 ^1 −(1/2)∫_0 ^1 ((ln(1+x^2 ))/(1+x))dx =(1/2)ln^2 (2)−(1/2)∫_0 ^1 ((ln(1+x^2 ))/(1+x))dx ∫_0 ^1 ((ln(1+x^2 ))/(1+x))dx =∫_0 ^1 ln(1+x^2 )Σ_(n=0) ^∞ (−1)^n x^n dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^n ln(1+x^2 )dx =Σ_(n=0) ^∞ (−1)^n u_n u_n =∫_0 ^1 x^n ln(1+x^2 )dx =[(x^(n+1) /(n+1))ln(1+x^2 )]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))×((2x)/(1+x^2 ))dx =((ln(2))/(n+1))−(2/(n+1))∫_0 ^1 (x^(n+2) /(1+x^2 )) dx .....be continued...

$$\mathrm{let}\:\mathrm{try}\:\mathrm{parametric}\:\mathrm{method}\:\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx}\:\mathrm{let} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{ax}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{ax}\right)\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{ax}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{ax}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\alpha}{\mathrm{ax}+\mathrm{1}}\:+\frac{\mathrm{mx}+\mathrm{n}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha=\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\mathrm{1}\right)}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:,\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xF}\left(\mathrm{x}\right)=\mathrm{0}\:=\frac{\alpha}{\mathrm{a}}\:+\mathrm{m}\:\Rightarrow\mathrm{m}=−\frac{\alpha}{\mathrm{a}}=−\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{0}\right)=\mathrm{1}\:=\alpha\:+\mathrm{n}\:\Rightarrow\mathrm{n}=\mathrm{1}−\alpha\:=\mathrm{1}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{ax}+\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{x}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}\:=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{ax}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ax}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\mathrm{ln}\left(\mathrm{ax}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\frac{\mathrm{a}}{\mathrm{2}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }.\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{a}+\mathrm{1}\right)−\frac{\mathrm{aln}\left(\mathrm{2}\right)}{\mathrm{2}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}+\frac{\pi}{\mathrm{4}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\int\:\:\frac{\mathrm{aln}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{da}\:−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\int\:\:\frac{\mathrm{ada}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:+\frac{\pi}{\mathrm{4}}\:\mathrm{arctana}\:+\mathrm{c} \\ $$$$=\int\:\:\frac{\mathrm{aln}\left(\mathrm{1}+\mathrm{a}\right)}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\mathrm{da}−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)+\frac{\pi}{\mathrm{4}}\:\mathrm{arctan}\left(\mathrm{a}\right)+\mathrm{C} \\ $$$$\int\:\:\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)\mathrm{da}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)−\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)\frac{\mathrm{da}}{\mathrm{1}+\mathrm{a}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{a}}\mathrm{da}\:\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}−\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)+\frac{\pi}{\mathrm{4}}\:\mathrm{arctan}\left(\mathrm{a}\right)\:+\mathrm{C} \\ $$$$\mathrm{C}=\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}−\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{4}}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:=\Phi \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{by}\:\mathrm{parts}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{u}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\:=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}×\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:.....\mathrm{be}\:\mathrm{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com