
Question Number 207652 by universe last updated on 22/May/24
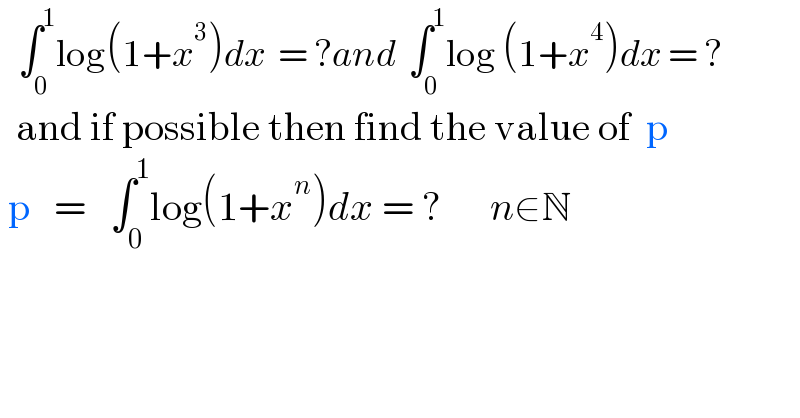
$$\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx}\:\:=\:?{and}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\:\left(\mathrm{1}+{x}^{\mathrm{4}} \right){dx}\:=\:? \\ $$$$\:\:\mathrm{and}\:\mathrm{if}\:\mathrm{possible}\:\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{p} \\ $$$$\:\mathrm{p}\:\:\:=\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\mathrm{1}+{x}^{{n}} \right){dx}\:=\:?\:\:\:\:\:\:{n}\in\mathbb{N} \\ $$
Answered by Berbere last updated on 22/May/24
![using x^n +1 =Π_(k=0) ^(n−1) (x−e^(i(2k+1)(π/n)) )=Π_(k=0) ^(n−1) ln(x−e^((i(2k+1)π)/n) ) ∫_0 ^1 ln(x−e^(i(((2k+1)π)/n))) )dx=ln(e^(i(π+((2k+1)/n)π)) (1−xe^((i(2k+1)π)/n) )) using principal log representation log(z)=ln∣z∣+iarg(z);arg(z)∈[−(π/2),((3π)/2)[ e^(i(π+((2k+1)/n)π)) =e^(i(−π+((2k+1)/n)π)) ;ln(e^(i(−π+((2k+1)/n)π)) )=i(−π+((2k+1)/n)π) p=Σ_(k=0) ^(n−1) i(−π+((2k+1)/n)π)+Σ_(k=0) ^(n−1) ∫_0 ^1 ln(1−xe^(−i(((2k+1)/n))π) )dx =Σ_(k=0) ^(n−1) ∫_0 ^1 ln(1−xe^(−i(((2k+1)/n))π) )dx ln(1−xa)]_0 ^1 =(1/a)((ax−1)ln(1−xa)−ax)]_0 ^1 =(1/a)(a−1)ln(1−a)−1 =Σ_(k=0) ^(n−1) e^(i(((2k+1)/n))π) [(e^(−i(((2k+1)/n))π) −1)ln(1−e^(−((iπ)/n)(2k+1)) )−1]](Q207660.png)
$${using}\:{x}^{{n}} +\mathrm{1}\:=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({x}−{e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{{n}}} \right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}{ln}\left({x}−{e}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}−{e}^{{i}\left(\frac{\left.\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}\right)} \right){dx}={ln}\left({e}^{{i}\left(\pi+\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\pi\right)} \left(\mathrm{1}−{xe}^{\frac{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{{n}}} \right)\right) \\ $$$${using}\:{principal}\:{log}\:{representation} \\ $$$${log}\left({z}\right)={ln}\mid{z}\mid+{iarg}\left({z}\right);{arg}\left({z}\right)\in\left[−\frac{\pi}{\mathrm{2}},\frac{\mathrm{3}\pi}{\mathrm{2}}\left[\right.\right. \\ $$$${e}^{{i}\left(\pi+\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\pi\right)} ={e}^{{i}\left(−\pi+\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\pi\right)} ;{ln}\left({e}^{{i}\left(−\pi+\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\pi\right)} \right)={i}\left(−\pi+\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\pi\right) \\ $$$${p}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{i}\left(−\pi+\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\pi\right)+\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{xe}^{−{i}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\right)\pi} \right){dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{xe}^{−{i}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\right)\pi} \right){dx} \\ $$$$\left.{l}\left.{n}\left(\mathrm{1}−{xa}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{a}}\left(\left({ax}−\mathrm{1}\right){ln}\left(\mathrm{1}−{xa}\right)−{ax}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{a}}\left({a}−\mathrm{1}\right){ln}\left(\mathrm{1}−{a}\right)−\mathrm{1} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{e}^{{i}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\right)\pi} \left[\left({e}^{−{i}\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}\right)\pi} −\mathrm{1}\right){ln}\left(\mathrm{1}−{e}^{−\frac{{i}\pi}{{n}}\left(\mathrm{2}{k}+\mathrm{1}\right)} \right)−\mathrm{1}\right] \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
