
Question Number 128721 by rs4089 last updated on 09/Jan/21
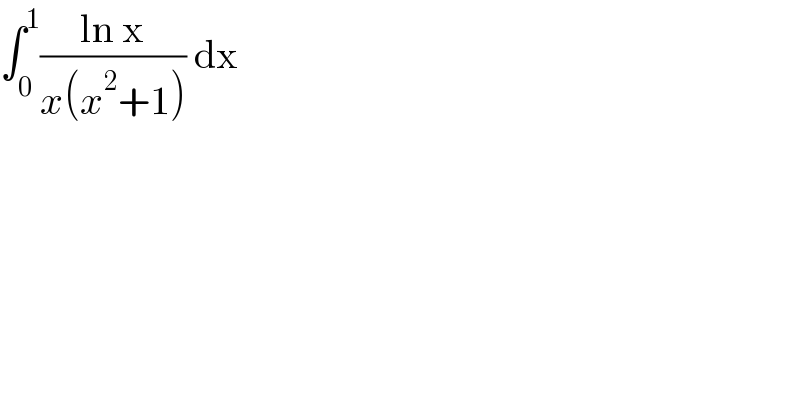
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\:\mathrm{x}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Jan/21
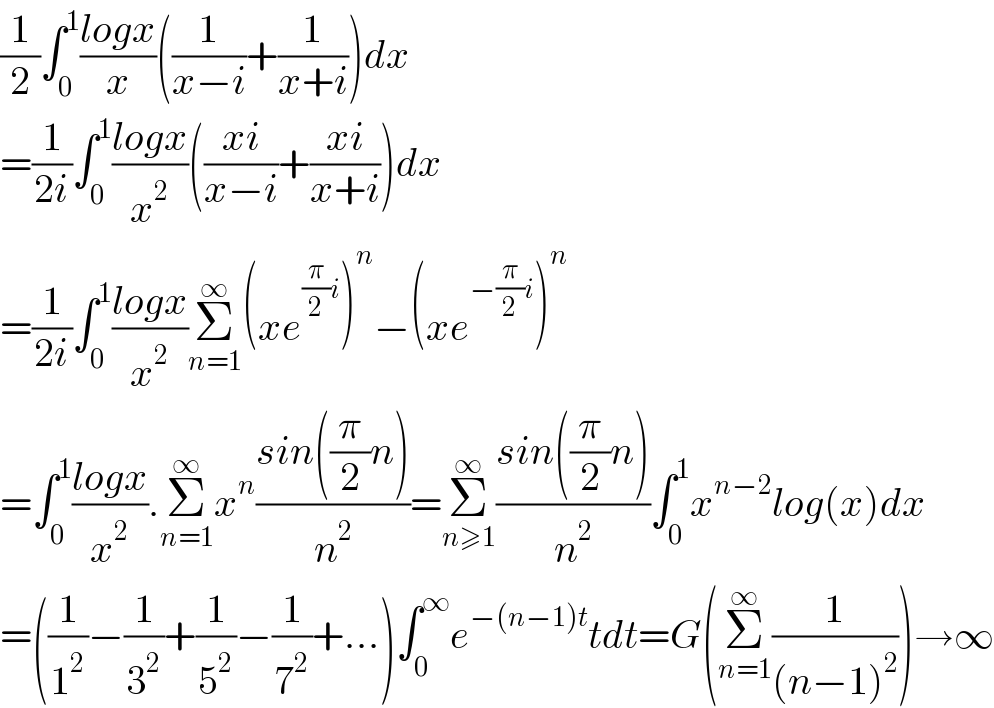
$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}}\left(\frac{\mathrm{1}}{{x}−{i}}+\frac{\mathrm{1}}{{x}+{i}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}^{\mathrm{2}} }\left(\frac{{xi}}{{x}−{i}}+\frac{{xi}}{{x}+{i}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}^{\mathrm{2}} }\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left({xe}^{\frac{\pi}{\mathrm{2}}{i}} \right)^{{n}} −\left({xe}^{−\frac{\pi}{\mathrm{2}}{i}} \right)^{{n}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}^{\mathrm{2}} }.\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}} \frac{{sin}\left(\frac{\pi}{\mathrm{2}}{n}\right)}{{n}^{\mathrm{2}} }=\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\frac{\pi}{\mathrm{2}}{n}\right)}{{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{2}} {log}\left({x}\right){dx} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+...\right)\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}−\mathrm{1}\right){t}} {tdt}={G}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right)\rightarrow\infty \\ $$
