Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 202731 by MrGHK last updated on 02/Jan/24

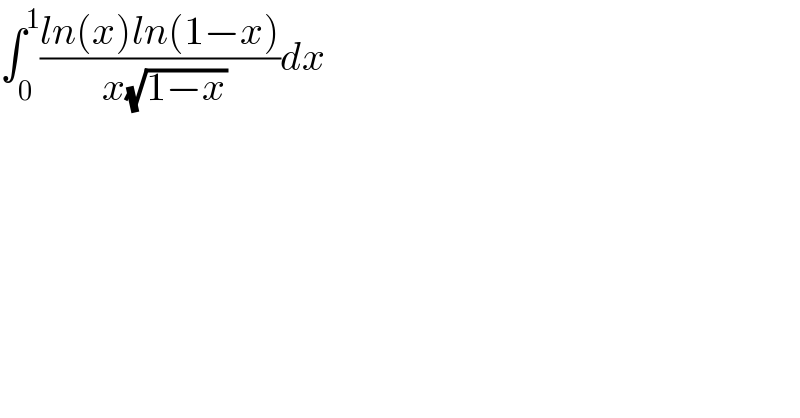
∫_0 ^1 ((ln(x)ln(1−x))/( x(√(1−x))))dx

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right)}{\:{x}\sqrt{\mathrm{1}−{x}}}{dx} \\ $$

Answered by witcher3 last updated on 02/Jan/24

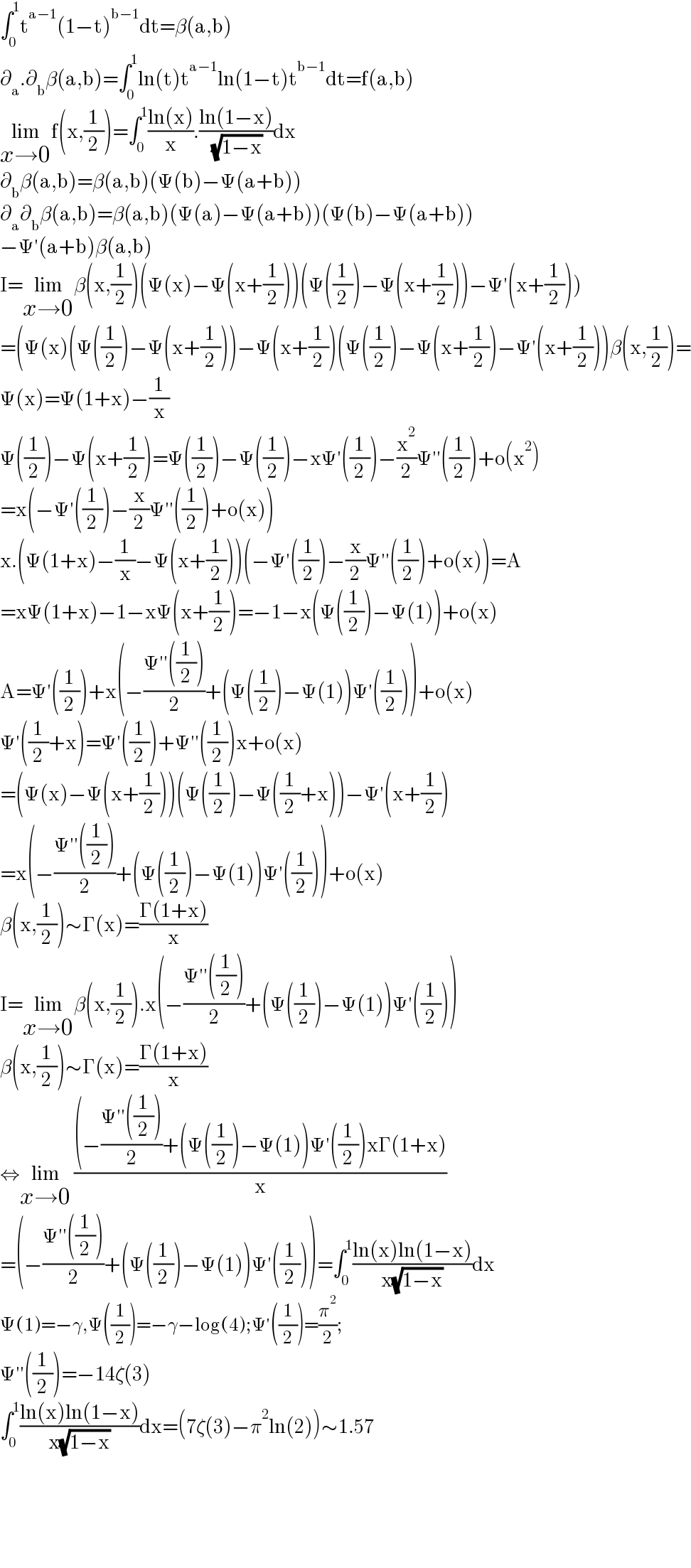
∫_0 ^1 t^(a−1) (1−t)^(b−1) dt=β(a,b) ∂_a .∂_b β(a,b)=∫_0 ^1 ln(t)t^(a−1) ln(1−t)t^(b−1) dt=f(a,b) lim_(x→0) f(x,(1/2))=∫_0 ^1 ((ln(x))/x).((ln(1−x))/( (√(1−x))))dx ∂_b β(a,b)=β(a,b)(Ψ(b)−Ψ(a+b)) ∂_a ∂_b β(a,b)=β(a,b)(Ψ(a)−Ψ(a+b))(Ψ(b)−Ψ(a+b)) −Ψ′(a+b)β(a,b) I=lim_(x→0) β(x,(1/2))(Ψ(x)−Ψ(x+(1/2)))(Ψ((1/2))−Ψ(x+(1/2)))−Ψ′(x+(1/2))) =(Ψ(x)(Ψ((1/2))−Ψ(x+(1/2)))−Ψ(x+(1/2))(Ψ((1/2))−Ψ(x+(1/2))−Ψ′(x+(1/2)))β(x,(1/2))= Ψ(x)=Ψ(1+x)−(1/x) Ψ((1/2))−Ψ(x+(1/2))=Ψ((1/2))−Ψ((1/2))−xΨ′((1/2))−(x^2 /2)Ψ′′((1/2))+o(x^2 ) =x(−Ψ′((1/2))−(x/2)Ψ′′((1/2))+o(x)) x.(Ψ(1+x)−(1/x)−Ψ(x+(1/2)))(−Ψ′((1/2))−(x/2)Ψ′′((1/2))+o(x))=A =xΨ(1+x)−1−xΨ(x+(1/2))=−1−x(Ψ((1/2))−Ψ(1))+o(x) A=Ψ′((1/2))+x(−((Ψ′′((1/2)))/2)+(Ψ((1/2))−Ψ(1))Ψ′((1/2)))+o(x) Ψ′((1/2)+x)=Ψ′((1/2))+Ψ′′((1/2))x+o(x) =(Ψ(x)−Ψ(x+(1/2)))(Ψ((1/2))−Ψ((1/2)+x))−Ψ′(x+(1/2)) =x(−((Ψ′′((1/2)))/2)+(Ψ((1/2))−Ψ(1))Ψ′((1/2)))+o(x) β(x,(1/2))∼Γ(x)=((Γ(1+x))/x) I=lim_(x→0) β(x,(1/2)).x(−((Ψ′′((1/2)))/2)+(Ψ((1/2))−Ψ(1))Ψ′((1/2))) β(x,(1/2))∼Γ(x)=((Γ(1+x))/x) ⇔lim_(x→0) (((−((Ψ′′((1/2)))/2)+(Ψ((1/2))−Ψ(1))Ψ′((1/2))xΓ(1+x))/x) =(−((Ψ′′((1/2)))/2)+(Ψ((1/2))−Ψ(1))Ψ′((1/2)))=∫_0 ^1 ((ln(x)ln(1−x))/(x(√(1−x))))dx Ψ(1)=−γ,Ψ((1/2))=−γ−log(4);Ψ′((1/2))=(π^2 /2); Ψ′′((1/2))=−14ζ(3) ∫_0 ^1 ((ln(x)ln(1−x))/(x(√(1−x))))dx=(7ζ(3)−π^2 ln(2))∼1.57

$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}^{\mathrm{a}−\mathrm{1}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{b}−\mathrm{1}} \mathrm{dt}=\beta\left(\mathrm{a},\mathrm{b}\right) \\ $$$$\partial_{\mathrm{a}} .\partial_{\mathrm{b}} \beta\left(\mathrm{a},\mathrm{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{t}^{\mathrm{a}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\mathrm{t}^{\mathrm{b}−\mathrm{1}} \mathrm{dt}=\mathrm{f}\left(\mathrm{a},\mathrm{b}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}f}\left(\mathrm{x},\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}}.\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\:\sqrt{\mathrm{1}−\mathrm{x}}}\mathrm{dx} \\ $$$$\partial_{\mathrm{b}} \beta\left(\mathrm{a},\mathrm{b}\right)=\beta\left(\mathrm{a},\mathrm{b}\right)\left(\Psi\left(\mathrm{b}\right)−\Psi\left(\mathrm{a}+\mathrm{b}\right)\right) \\ $$$$\partial_{\mathrm{a}} \partial_{\mathrm{b}} \beta\left(\mathrm{a},\mathrm{b}\right)=\beta\left(\mathrm{a},\mathrm{b}\right)\left(\Psi\left(\mathrm{a}\right)−\Psi\left(\mathrm{a}+\mathrm{b}\right)\right)\left(\Psi\left(\mathrm{b}\right)−\Psi\left(\mathrm{a}+\mathrm{b}\right)\right) \\ $$$$−\Psi'\left(\mathrm{a}+\mathrm{b}\right)\beta\left(\mathrm{a},\mathrm{b}\right) \\ $$$$\left.\mathrm{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\beta\left(\mathrm{x},\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\Psi\left(\mathrm{x}\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\Psi'\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=\left(\Psi\left(\mathrm{x}\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi'\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\beta\left(\mathrm{x},\frac{\mathrm{1}}{\mathrm{2}}\right)=\right. \\ $$$$\Psi\left(\mathrm{x}\right)=\Psi\left(\mathrm{1}+\mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{x}\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{x}\left(−\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{x}}{\mathrm{2}}\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{o}\left(\mathrm{x}\right)\right) \\ $$$$\mathrm{x}.\left(\Psi\left(\mathrm{1}+\mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{x}}−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\left(−\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{x}}{\mathrm{2}}\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{o}\left(\mathrm{x}\right)\right)=\mathrm{A} \\ $$$$=\mathrm{x}\Psi\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{1}−\mathrm{x}\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{1}−\mathrm{x}\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)+\mathrm{o}\left(\mathrm{x}\right) \\ $$$$\mathrm{A}=\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{x}\left(−\frac{\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}+\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+\mathrm{o}\left(\mathrm{x}\right) \\ $$$$\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{x}\right)=\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}+\mathrm{o}\left(\mathrm{x}\right) \\ $$$$=\left(\Psi\left(\mathrm{x}\right)−\Psi\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{x}\right)\right)−\Psi'\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\mathrm{x}\left(−\frac{\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}+\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+\mathrm{o}\left(\mathrm{x}\right) \\ $$$$\beta\left(\mathrm{x},\frac{\mathrm{1}}{\mathrm{2}}\right)\sim\Gamma\left(\mathrm{x}\right)=\frac{\Gamma\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}} \\ $$$$\mathrm{I}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\beta\left(\mathrm{x},\frac{\mathrm{1}}{\mathrm{2}}\right).\mathrm{x}\left(−\frac{\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}+\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\beta\left(\mathrm{x},\frac{\mathrm{1}}{\mathrm{2}}\right)\sim\Gamma\left(\mathrm{x}\right)=\frac{\Gamma\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}} \\ $$$$\Leftrightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(−\frac{\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}+\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}\Gamma\left(\mathrm{1}+\mathrm{x}\right)\right.}{\mathrm{x}} \\ $$$$=\left(−\frac{\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}+\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}}}\mathrm{dx} \\ $$$$\Psi\left(\mathrm{1}\right)=−\gamma,\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma−\mathrm{log}\left(\mathrm{4}\right);\Psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}; \\ $$$$\Psi''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{14}\zeta\left(\mathrm{3}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}\sqrt{\mathrm{1}−\mathrm{x}}}\mathrm{dx}=\left(\mathrm{7}\zeta\left(\mathrm{3}\right)−\pi^{\mathrm{2}} \mathrm{ln}\left(\mathrm{2}\right)\right)\sim\mathrm{1}.\mathrm{57} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by MrGHK last updated on 03/Jan/24

nice solution sir

$$\mathrm{nice}\:\mathrm{solution}\:\mathrm{sir} \\ $$

Commented by witcher3 last updated on 08/Jan/24

thanx have a nice day

$$\mathrm{thanx}\:\mathrm{have}\:\mathrm{a}\:\mathrm{nice}\:\mathrm{day} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com