
Question Number 163357 by mnjuly1970 last updated on 06/Jan/22
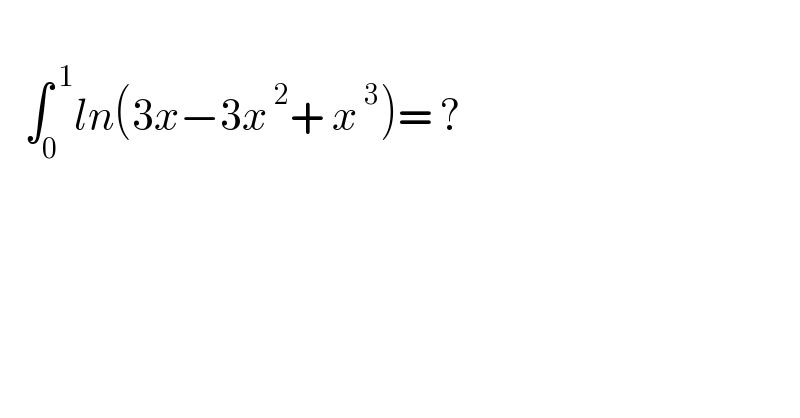
$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\mathrm{3}{x}−\mathrm{3}{x}^{\:\mathrm{2}} +\:{x}^{\:\mathrm{3}} \right)=\:? \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 06/Jan/22
![I=∫_0 ^1 ln(3x−3x^2 +x^3 )dx =∫_0 ^1 lnxdx+∫_0 ^1 ln(x^2 −3x+3)dx =[xlnx−x]_0 ^1 +[xln(x^2 −3x+3)]_0 ^1 −∫_0 ^1 ((2x^2 −3x)/(x^2 −3x+3))dx =−1−∫_0 ^1 (2+((3x−6)/(x^2 −3x+3)))dx=−1−2−∫_0 ^1 ((3x−6)/(x^2 −3x+3))dx =−3−(3/2)∫_0 ^1 (((2x−3)/(x^2 −3x+3))−(1/(x^2 −3x+3)))dx =−3−(3/2)[ln(x^2 −3x+3)]_0 ^1 +(3/2)∫_0 ^1 (dx/((x−(3/2))^2 +(3/4))) =−3+(3/2)ln3+(√3)[arctan(((2x−3)/( (√3))))]_0 ^1 =−3+(3/2)ln3+(√3)(−(π/6)+(π/3))=−3+(3/2)ln3+(π/(2(√3)))](Q163363.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{3}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right){dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}{xdx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right){dx} \\ $$$$\:\:\:=\left[{x}\mathrm{ln}{x}−{x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[{x}\mathrm{ln}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}{dx} \\ $$$$\:\:\:=−\mathrm{1}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}+\frac{\mathrm{3}{x}−\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}\right){dx}=−\mathrm{1}−\mathrm{2}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{3}{x}−\mathrm{6}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}{dx} \\ $$$$\:\:\:=−\mathrm{3}−\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{3}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}}\right){dx} \\ $$$$\:\:\:=−\mathrm{3}−\frac{\mathrm{3}}{\mathrm{2}}\left[\mathrm{ln}\left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:\:=−\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln3}+\sqrt{\mathrm{3}}\left[\mathrm{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{3}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:=−\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln3}+\sqrt{\mathrm{3}}\left(−\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{3}}\right)=−\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln3}+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$
Commented by mnjuly1970 last updated on 06/Jan/22
$$\:\:{mercey}\:\:{mr}\:{brandon}.. \\ $$
