Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 217441 by mr W last updated on 13/Mar/25

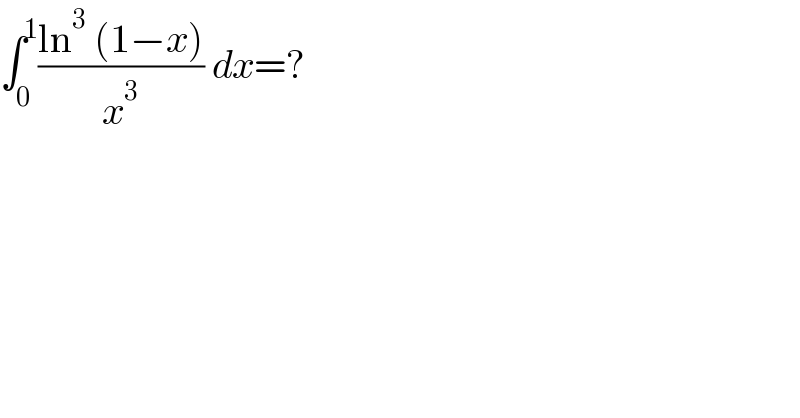
∫_0 ^1 ((ln^3 (1−x))/x^3 ) dx=?

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \:\left(\mathrm{1}−{x}\right)}{{x}^{\mathrm{3}} }\:{dx}=? \\ $$

Answered by MrGaster last updated on 14/Mar/25

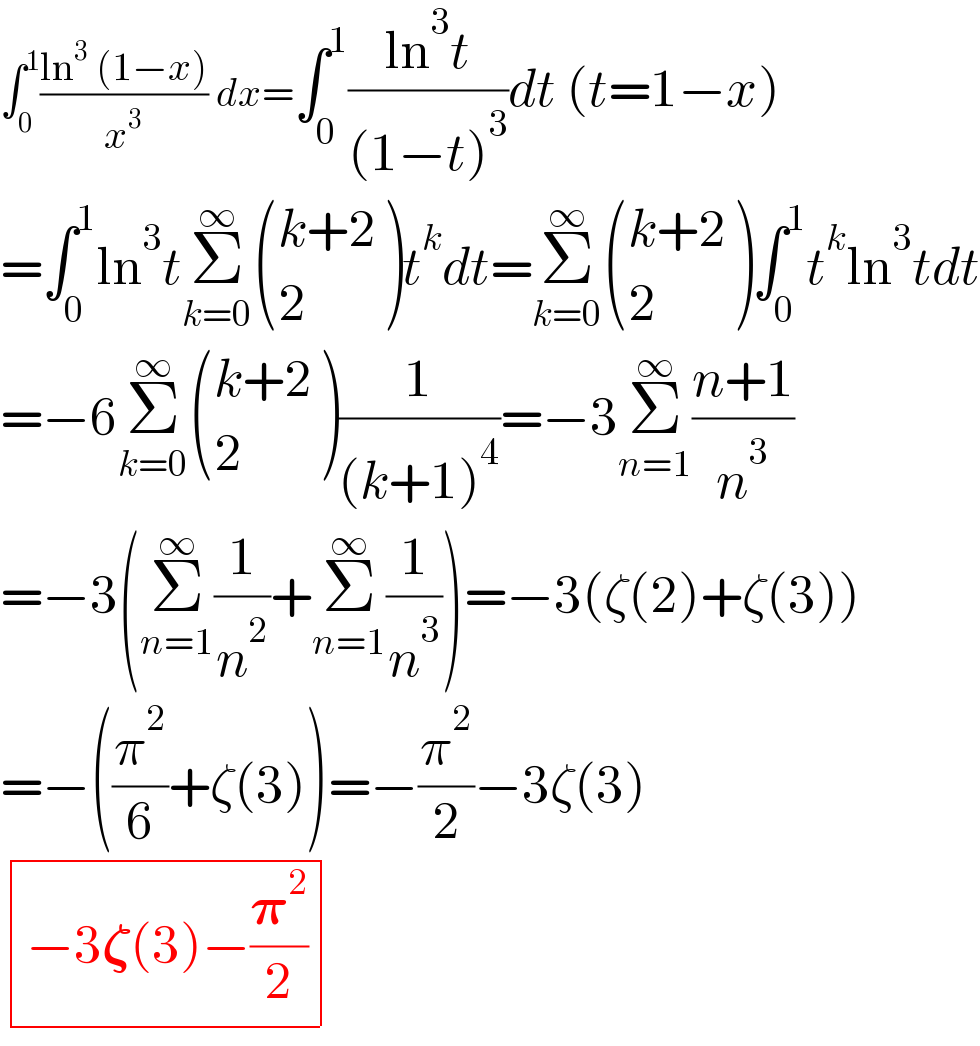
∫_0 ^1 ((ln^3 (1−x))/x^3 ) dx=∫_0 ^1 ((ln^3 t)/((1−t)^3 ))dt (t=1−x) =∫_0 ^1 ln^3 tΣ_(k=0) ^∞ (((k+2)),(2) )t^k dt=Σ_(k=0) ^∞ (((k+2)),(2) )∫_0 ^1 t^k ln^3 tdt =−6Σ_(k=0) ^∞ (((k+2)),(2) )(1/((k+1)^4 ))=−3Σ_(n=1) ^∞ ((n+1)/n^3 ) =−3(Σ_(n=1) ^∞ (1/n^2 )+Σ_(n=1) ^∞ (1/n^3 ))=−3(ζ(2)+ζ(3)) =−((π^2 /6)+ζ(3))=−(π^2 /2)−3ζ(3) determinant (((−3𝛇(3)−(𝛑^2 /2))))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \:\left(\mathrm{1}−{x}\right)}{{x}^{\mathrm{3}} }\:{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} {t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{3}} }{dt}\:\left({t}=\mathrm{1}−{x}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{3}} {t}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{{k}+\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}{t}^{{k}} {dt}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{{k}+\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{k}} \mathrm{ln}^{\mathrm{3}} {tdt} \\ $$$$=−\mathrm{6}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{{k}+\mathrm{2}}\\{\mathrm{2}}\end{pmatrix}\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{4}} }=−\mathrm{3}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$=−\mathrm{3}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)=−\mathrm{3}\left(\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)\right) \\ $$$$=−\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\zeta\left(\mathrm{3}\right)\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\mathrm{3}\zeta\left(\mathrm{3}\right) \\ $$$$\begin{array}{|c|}{−\mathrm{3}\boldsymbol{\zeta}\left(\mathrm{3}\right)−\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{2}}}\\\hline\end{array} \\ $$

Commented by mr W last updated on 14/Mar/25

��

Commented by mr W last updated on 14/Mar/25

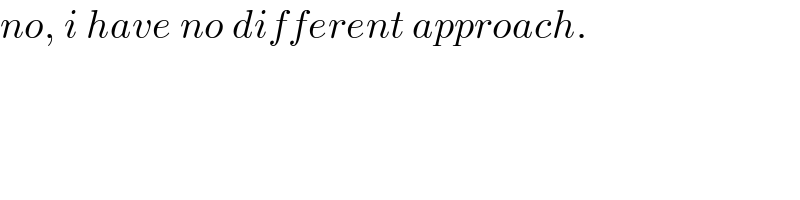
no, i have no different approach.

$${no},\:{i}\:{have}\:{no}\:{different}\:{approach}. \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Sir mrW. What of your approach sir. Is your approach the same as this?. If it is different, please solve when you are chanced sir. Thanks for everytime sir.

$$\mathrm{Sir}\:\mathrm{mrW}. \\ $$$$\mathrm{What}\:\mathrm{of}\:\mathrm{your}\:\mathrm{approach}\:\mathrm{sir}. \\ $$$$\mathrm{Is}\:\mathrm{your}\:\mathrm{approach}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{this}?. \\ $$$$\mathrm{If}\:\mathrm{it}\:\mathrm{is}\:\mathrm{different},\:\mathrm{please}\:\mathrm{solve}\:\mathrm{when}\:\mathrm{you} \\ $$$$\mathrm{are}\:\mathrm{chanced}\:\mathrm{sir}. \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{everytime}\:\mathrm{sir}. \\ $$

Answered by mr W last updated on 14/Mar/25

=∫_0 ^1 ((ln^3 t)/((1−t)^3 )) dt =∫_0 ^1 ln^3 t Σ_(n=2) ^∞ (((n−1)n)/2)t^(n−2) dt =Σ_(n=2) ^∞ (((n−1)n)/2)∫_0 ^1 ln^3 t t^(n−2) dt =Σ_(n=0) ^∞ (((n+1)(n+2))/2)∫_0 ^1 ln^3 t t^n dt I=∫_0 ^1 ln^3 t t^n dt =(1/(n+1))∫_0 ^1 ln^3 t dt^(n+1) =(1/(n+1)){[ln^3 t t^(n+1) ]_0 ^1 −3∫_0 ^1 ln^2 t t^n dt} =−(3/((n+1)^2 ))∫_0 ^1 ln^2 t dt^(n+1) =−(3/((n+1)^2 )){[ln^2 t t^(n+1) ]_0 ^1 −2∫_0 ^1 ln t t^n dt} =(6/((n+1)^3 ))∫_0 ^1 ln t dt^(n+1) =(6/((n+1)^3 )){[ln t t^(n+1) ]_0 ^1 −∫_0 ^1 t^n dt} =−(6/((n+1)^4 ))[ t^(n+1) ]_0 ^1 =−(6/((n+1)^4 )) ∫_0 ^1 ((ln^3 (1−x))/x^3 ) dx =−Σ_(n=0) ^∞ (((n+1)(n+2))/2)×(6/((n+1)^4 )) =−3Σ_(n=0) ^∞ ((n+2)/((n+1)^3 )) =−3(Σ_(n=0) ^∞ (1/((n+1)^2 ))+Σ_(n=0) ^∞ (1/((n+1)^3 ))) =−3(Σ_(n=1) ^∞ (1/n^2 )+Σ_(n=1) ^∞ (1/n^3 )) =−3[ζ(2)+ζ(3)]≈−8.5409729

$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \:{t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{3}} }\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{3}} \:{t}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}{t}^{{n}−\mathrm{2}} {dt} \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{3}} \:{t}\:{t}^{{n}−\mathrm{2}} {dt} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{3}} \:{t}\:{t}^{{n}} {dt} \\ $$$$ \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{3}} \:{t}\:{t}^{{n}} {dt} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{3}} \:{t}\:{dt}^{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left\{\left[\mathrm{ln}^{\mathrm{3}} \:{t}\:{t}^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \:{t}\:{t}^{{n}} {dt}\right\} \\ $$$$=−\frac{\mathrm{3}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \:{t}\:{dt}^{{n}+\mathrm{1}} \\ $$$$=−\frac{\mathrm{3}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\left\{\left[\mathrm{ln}^{\mathrm{2}} \:{t}\:{t}^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\:{t}\:{t}^{{n}} {dt}\right\} \\ $$$$=\frac{\mathrm{6}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\:{t}\:{dt}^{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{6}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }\left\{\left[\mathrm{ln}\:{t}\:{t}^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}} {dt}\right\} \\ $$$$=−\frac{\mathrm{6}}{\left({n}+\mathrm{1}\right)^{\mathrm{4}} }\left[\:{t}^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{6}}{\left({n}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \:\left(\mathrm{1}−{x}\right)}{{x}^{\mathrm{3}} }\:{dx} \\ $$$$=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}}×\frac{\mathrm{6}}{\left({n}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=−\mathrm{3}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}+\mathrm{2}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=−\mathrm{3}\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }\right) \\ $$$$=−\mathrm{3}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right) \\ $$$$=−\mathrm{3}\left[\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{3}\right)\right]\approx−\mathrm{8}.\mathrm{5409729} \\ $$

Commented by Tawa11 last updated on 14/Mar/25

Thanks sir. Weldone sir

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com