
Question Number 140866 by liberty last updated on 13/May/21
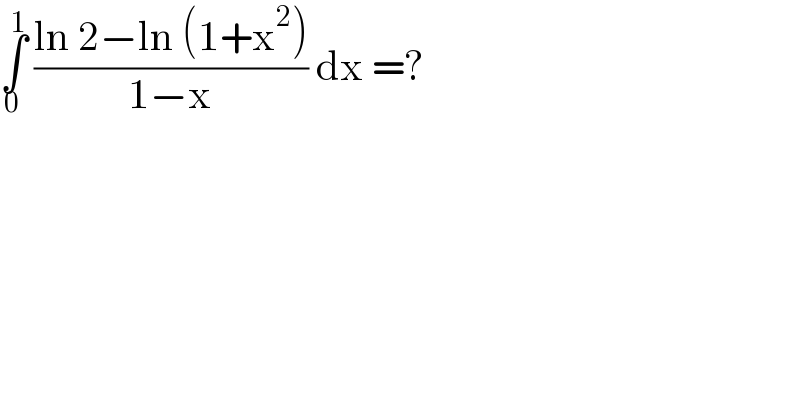
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{ln}\:\mathrm{2}−\mathrm{ln}\:\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{x}}\:\mathrm{dx}\:=?\: \\ $$
Answered by mindispower last updated on 15/May/21

$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\int_{\mathrm{0}} ^{{x}} \frac{{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}−{t}}{dt} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−{ln}\left(\mathrm{2}\right){ln}\left(\mathrm{1}−{x}\right)+{ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\int_{\mathrm{0}} ^{{x}} \frac{{ln}\left(\mathrm{1}−{t}\right)\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}{ln}\left(\mathrm{1}−{x}\right).{ln}\left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{2}}\right)=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}{ln}\left(\mathrm{1}−\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{2}}\right){ln}\left(\mathrm{1}−{x}\right)=\mathrm{0} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right).\mathrm{2}{xdx}}{\mathrm{1}+{x}^{\mathrm{2}} }=−{A} \\ $$$${let}\:{B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right).\mathrm{2}{xdx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${A}+{B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }.{d}\left({x}^{\mathrm{2}} \right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{\mathrm{1}+{t}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\mathrm{2}−{t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left(\mathrm{2}{w}\right)}{\mathrm{1}−{w}}.{dw}={ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{ln}\left({w}\right)}{\mathrm{1}−{w}}{dw} \\ $$$$={ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}={ln}^{\mathrm{2}} \left(\mathrm{2}\right)+{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{li}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$$${A}−{B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right).\mathrm{2}{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} },{t}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$${dt}=\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} }.\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right){ln}\left({x}\right)}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}−\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{ln}\left({x}\right){dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}{dx}=\frac{\mathrm{3}}{\mathrm{4}}.−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\left(−{x}\right)\right)}{−{x}}.{d}\left(−{x}\right) \\ $$$$=−\int_{\mathrm{0}} ^{−\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt}=\frac{−\mathrm{3}}{\mathrm{4}}{li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$
