
Question Number 160281 by amin96 last updated on 27/Nov/21
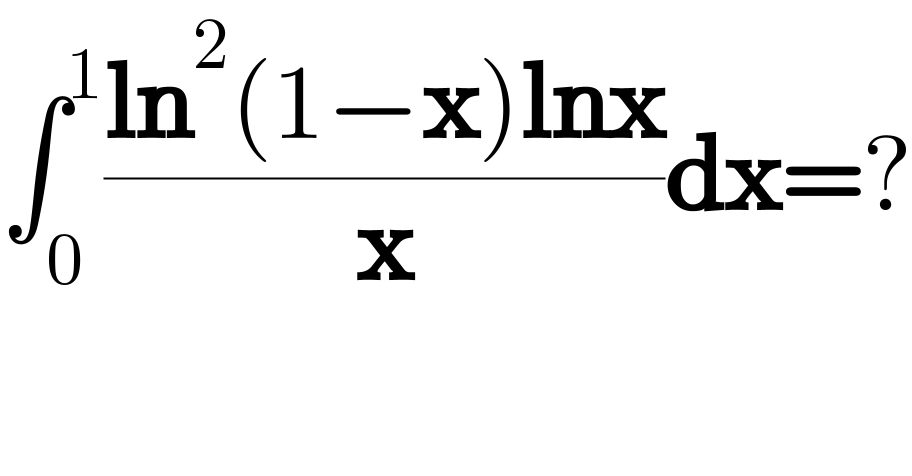
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{ln}}^{\mathrm{2}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{lnx}}}{\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}}=? \\ $$
Answered by TheSupreme last updated on 27/Nov/21
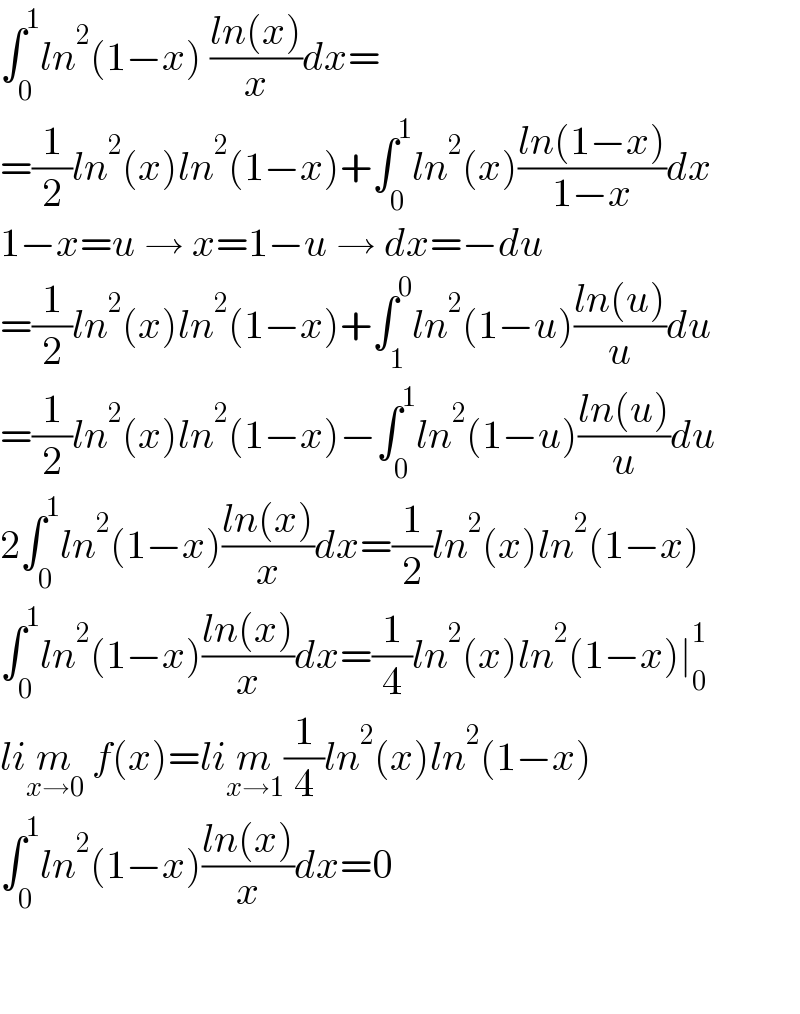
$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\:\frac{{ln}\left({x}\right)}{{x}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left({x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left({x}\right)\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}}{dx} \\ $$$$\mathrm{1}−{x}={u}\:\rightarrow\:{x}=\mathrm{1}−{u}\:\rightarrow\:{dx}=−{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left({x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)+\int_{\mathrm{1}} ^{\mathrm{0}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{u}\right)\frac{{ln}\left({u}\right)}{{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left({x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{u}\right)\frac{{ln}\left({u}\right)}{{u}}{du} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\frac{{ln}\left({x}\right)}{{x}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left({x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\frac{{ln}\left({x}\right)}{{x}}{dx}=\frac{\mathrm{1}}{\mathrm{4}}{ln}^{\mathrm{2}} \left({x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\:{f}\left({x}\right)={li}\underset{{x}\rightarrow\mathrm{1}} {{m}}\frac{\mathrm{1}}{\mathrm{4}}{ln}^{\mathrm{2}} \left({x}\right){ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\frac{{ln}\left({x}\right)}{{x}}{dx}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
