
Question Number 86646 by Ar Brandon last updated on 30/Mar/20
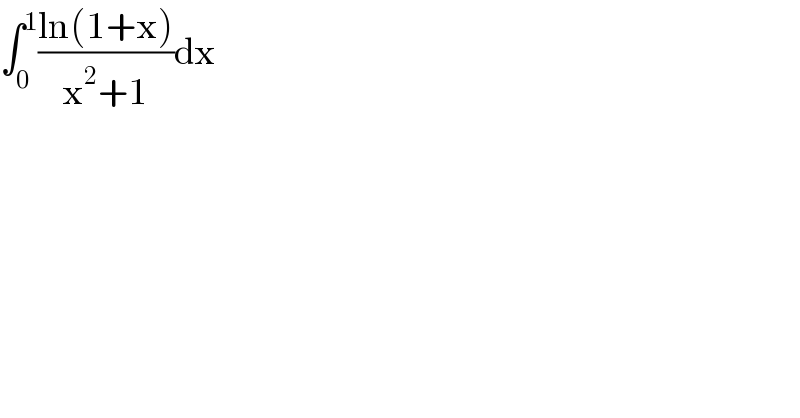
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20
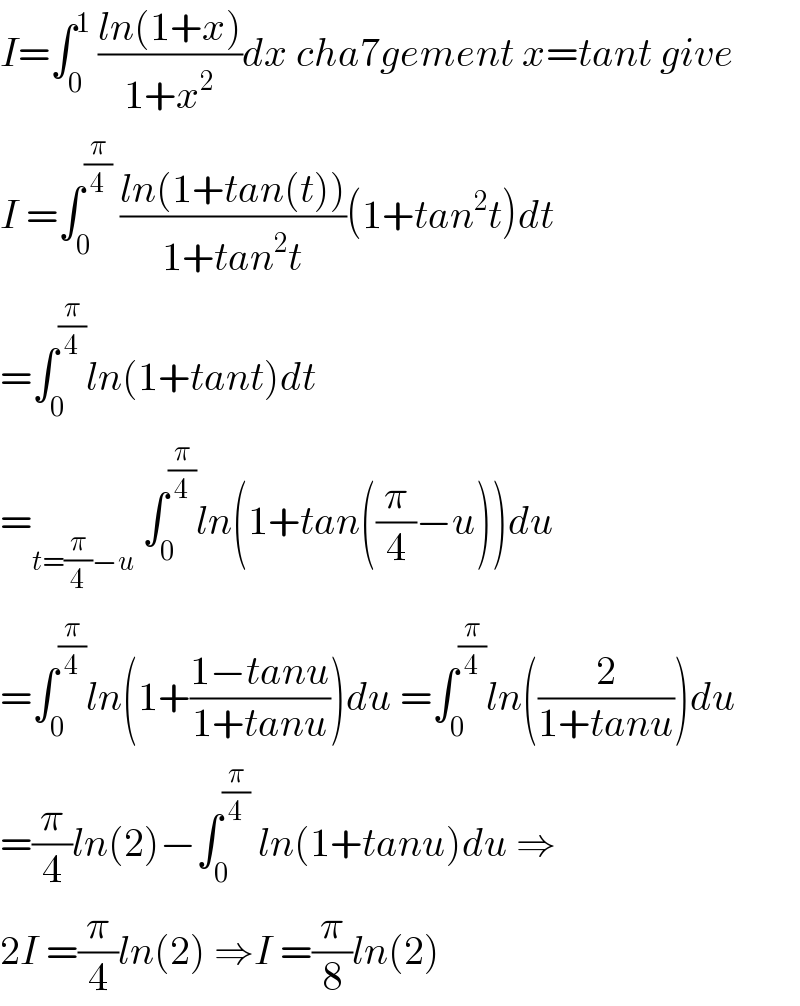
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{cha}\mathrm{7}{gement}\:{x}={tant}\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{ln}\left(\mathrm{1}+{tan}\left({t}\right)\right)}{\mathrm{1}+{tan}^{\mathrm{2}} {t}}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tant}\right){dt}\: \\ $$$$=_{{t}=\frac{\pi}{\mathrm{4}}−{u}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{u}\right)\right){du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tanu}}{\mathrm{1}+{tanu}}\right){du}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tanu}}\right){du} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}+{tanu}\right){du}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:\Rightarrow{I}\:=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$
Commented by Ar Brandon last updated on 30/Mar/20

$${cool}!! \\ $$$$ \\ $$
