
Question Number 149077 by mnjuly1970 last updated on 02/Aug/21
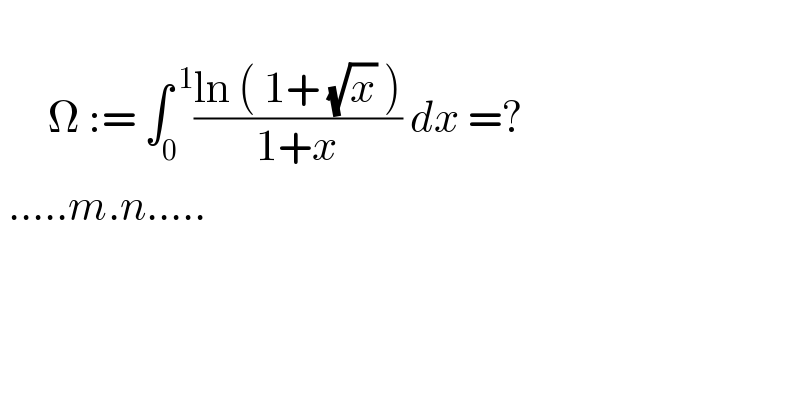
$$ \\ $$$$\:\:\:\:\:\:\Omega\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\:\left(\:\mathrm{1}+\:\sqrt{{x}}\:\right)}{\mathrm{1}+{x}}\:{dx}\:=? \\ $$$$\:.....{m}.{n}..... \\ $$
Answered by mindispower last updated on 02/Aug/21
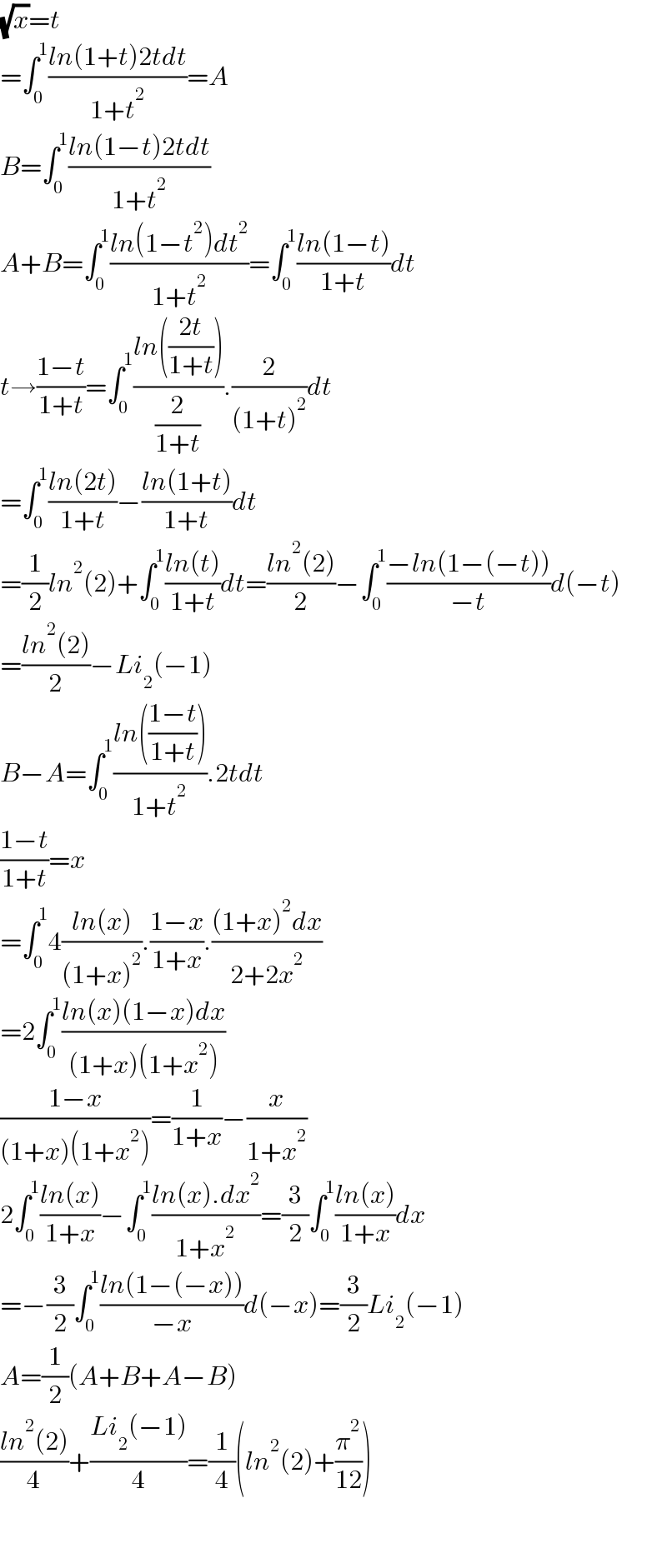
$$\sqrt{{x}}={t} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{t}\right)\mathrm{2}{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} }={A} \\ $$$${B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)\mathrm{2}{tdt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${A}+{B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$${t}\rightarrow\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}}\right)}{\frac{\mathrm{2}}{\mathrm{1}+{t}}}.\frac{\mathrm{2}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{2}{t}\right)}{\mathrm{1}+{t}}−\frac{{ln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\mathrm{1}+{t}}{dt}=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{ln}\left(\mathrm{1}−\left(−{t}\right)\right)}{−{t}}{d}\left(−{t}\right) \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−{Li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$$${B}−{A}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }.\mathrm{2}{tdt} \\ $$$$\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}}={x} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}\frac{{ln}\left({x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }.\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}.\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} {dx}}{\mathrm{2}+\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)\left(\mathrm{1}−{x}\right){dx}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}−{x}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{1}+{x}}−\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right).{dx}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\left(−{x}\right)\right)}{−{x}}{d}\left(−{x}\right)=\frac{\mathrm{3}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left({A}+{B}+{A}−{B}\right) \\ $$$$\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{4}}+\frac{{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}\left({ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 02/Aug/21
$$\:\:\:{thanks}\:{alot}\:{sir}\:{power}.... \\ $$
Commented by Tawa11 last updated on 02/Aug/21

$$\mathrm{weldone}\:\mathrm{sir}. \\ $$
Commented by mindispower last updated on 03/Aug/21

$${withe}\:{pleasur} \\ $$$$ \\ $$
