
Question Number 99818 by Ar Brandon last updated on 23/Jun/20
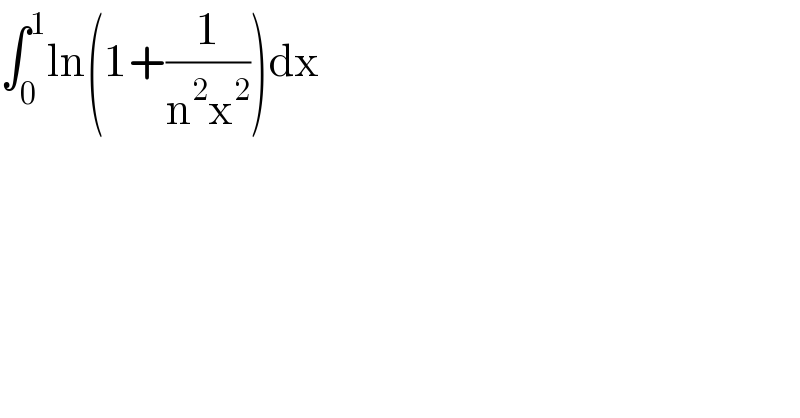
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$
Answered by smridha last updated on 23/Jun/20
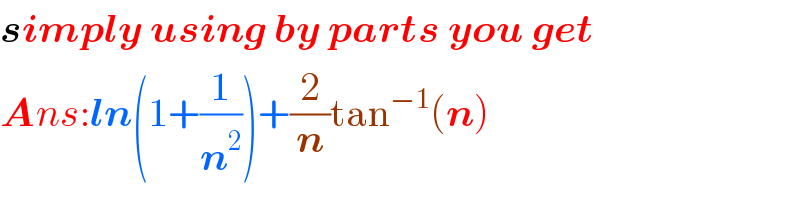
$$\boldsymbol{{simply}}\:\boldsymbol{{using}}\:\boldsymbol{{by}}\:\boldsymbol{{parts}}\:\boldsymbol{{you}}\:\boldsymbol{{get}} \\ $$$$\boldsymbol{{A}}{ns}:\boldsymbol{{ln}}\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{n}}^{\mathrm{2}} }\right)+\frac{\mathrm{2}}{\boldsymbol{{n}}}\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{n}}\right) \\ $$
Commented by Ar Brandon last updated on 23/Jun/20

$$\mathbb{THANKS} \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
![changement (1/(nx)) =t give nx =(1/t) ⇒x =(1/(nt)) ⇒dx =−(1/(nt^2 ))dt ⇒ I=∫_0 ^1 ln(1+(1/(n^2 t^2 )))dx =∫_(1/n) ^(+∞) ln(1+t^2 )(dt/(nt^2 )) =(1/n) ∫_(1/n) ^(+∞) ((ln(1+t^2 ))/t^2 ) dt by parts ∫_(1/n) ^(+∞) ((ln(1+t^2 ))/t^2 )dt =[−(1/t)ln(1+t^2 )]_(1/n) ^(+∞) +∫_(1/n) ^(+∞) (1/t)×((2t)/(1+t^2 ))dt =nln(1+(1/n^2 )) +2 [arctant]_(1/n) ^(+∞) =n ln(1+(1/n^2 ))+2{(π/2) −arctan((1/n))} =n ln(1+(1/n^2 )) +2arctan(n) ⇒I =ln(1+(1/n^2 ))+((2arctan(n))/n)](Q99837.png)
$$\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{nx}}\:=\mathrm{t}\:\mathrm{give}\:\mathrm{nx}\:=\frac{\mathrm{1}}{\mathrm{t}}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{nt}}\:\Rightarrow\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{nt}^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} }\right)\mathrm{dx}\:=\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{+\infty} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\frac{\mathrm{dt}}{\mathrm{nt}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{n}}\:\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{+\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{+\infty} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\right]_{\frac{\mathrm{1}}{\mathrm{n}}} ^{+\infty} \:+\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{+\infty} \:\frac{\mathrm{1}}{\mathrm{t}}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:+\mathrm{2}\:\:\left[\mathrm{arctant}\right]_{\frac{\mathrm{1}}{\mathrm{n}}} ^{+\infty} \:=\mathrm{n}\:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)+\mathrm{2}\left\{\frac{\pi}{\mathrm{2}}\:−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right\} \\ $$$$=\mathrm{n}\:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:+\mathrm{2arctan}\left(\mathrm{n}\right)\:\Rightarrow\mathrm{I}\:=\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)+\frac{\mathrm{2arctan}\left(\mathrm{n}\right)}{\mathrm{n}} \\ $$
Commented by Ar Brandon last updated on 23/Jun/20
cool, thanks
