
Question Number 100047 by Ar Brandon last updated on 24/Jun/20

$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$
Answered by smridha last updated on 24/Jun/20

$$=\frac{\sqrt{\boldsymbol{\pi}}}{\mathrm{2}}{erf}\left(\mathrm{1}\right) \\ $$
Commented by Ar Brandon last updated on 24/Jun/20
Thanks, but how do we arrive there ? Or is it just a theory ?
Commented by smridha last updated on 24/Jun/20
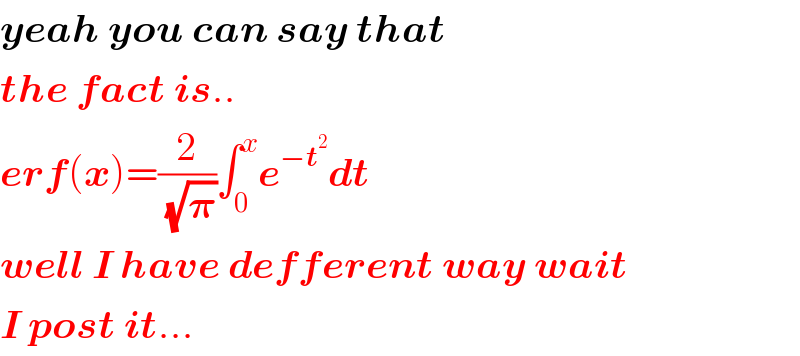
$$\boldsymbol{{yeah}}\:\boldsymbol{{you}}\:\boldsymbol{{can}}\:\boldsymbol{{say}}\:\boldsymbol{{that}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{fact}}\:\boldsymbol{{is}}.. \\ $$$$\boldsymbol{{erf}}\left(\boldsymbol{{x}}\right)=\frac{\mathrm{2}}{\sqrt{\boldsymbol{\pi}}}\int_{\mathrm{0}} ^{{x}} \boldsymbol{{e}}^{−\boldsymbol{{t}}^{\mathrm{2}} } \boldsymbol{{dt}} \\ $$$$\boldsymbol{{well}}\:\boldsymbol{{I}}\:\boldsymbol{{have}}\:\boldsymbol{{defferent}}\:\boldsymbol{{way}}\:\boldsymbol{{wait}} \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{post}}\:\boldsymbol{{it}}... \\ $$
Answered by smridha last updated on 24/Jun/20
![=∫_0 ^1 Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!))dx =1.Σ_(n=0) ^∞ (((−1)^n )/(n!(2n+1))) =Σ_(n=0) ^∞ ((1/2)/((n+(1/2)))).(((−1)^n )/(n!)) =Σ_(n=0 ) ^∞ ((((1/2))_n )/(((3/2))_n )).(((−1)^n )/(n!)) =M((1/2),(3/2),−1)or _1 F_1 ((1/2);(3/2);−1) this is called confluent hypergeometric f^n . note:(a)=(((a)_n )/((a+1)_n ))(a+n)[pochhammer symbol]](Q100060.png)
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \boldsymbol{{x}}^{\mathrm{2}\boldsymbol{{n}}} }{\boldsymbol{{n}}!}\boldsymbol{{dx}} \\ $$$$=\mathrm{1}.\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)} \\ $$$$=\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\left(\boldsymbol{{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}.\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!} \\ $$$$=\underset{\boldsymbol{{n}}=\mathrm{0}\:} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{\boldsymbol{{n}}} }{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)_{\boldsymbol{{n}}} }.\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!} \\ $$$$=\boldsymbol{{M}}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}},−\mathrm{1}\right)\boldsymbol{{or}}\:_{\mathrm{1}} \boldsymbol{{F}}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}};\frac{\mathrm{3}}{\mathrm{2}};−\mathrm{1}\right) \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{called}}\:\boldsymbol{{confluent}}\:\boldsymbol{{hypergeometric}} \\ $$$$\boldsymbol{{f}}^{\boldsymbol{{n}}} . \\ $$$$\boldsymbol{{note}}:\left(\boldsymbol{{a}}\right)=\frac{\left(\boldsymbol{{a}}\right)_{\boldsymbol{{n}}} }{\left(\boldsymbol{{a}}+\mathrm{1}\right)_{\boldsymbol{{n}}} }\left(\boldsymbol{{a}}+\boldsymbol{{n}}\right)\left[\boldsymbol{{pochhammer}}\:\boldsymbol{{symbol}}\right] \\ $$
Commented by Ar Brandon last updated on 24/Jun/20
Thanks so very much��
