
Question Number 165615 by cortano1 last updated on 05/Feb/22
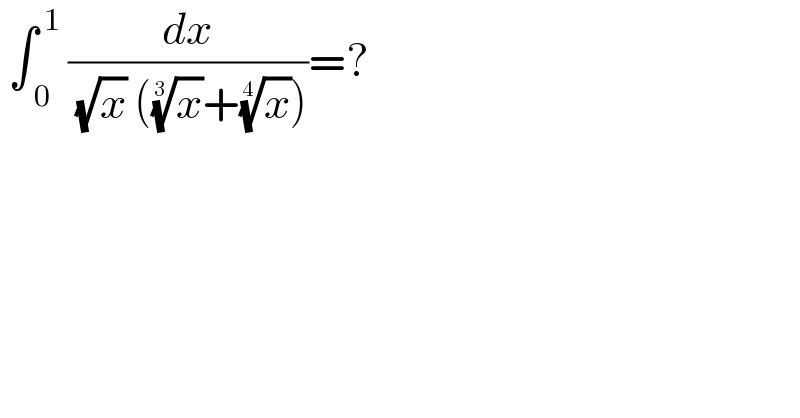
$$\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{dx}}{\:\sqrt{{x}}\:\left(\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{4}}]{{x}}\right)}=? \\ $$
Answered by Ar Brandon last updated on 05/Feb/22
![I=∫_0 ^1 (dx/( (√x)((x)^(1/3) +(x)^(1/4) ))) , x=t^(12) ⇒dx=12t^(11) dt =12∫_0 ^1 (t^(11) /(t^6 (t^4 +t^3 )))=12∫_0 ^1 (t^2 /(t+1))dt=12∫_0 ^1 (((t+1−1)^2 )/(t+1))dt =12∫_0 ^1 (t+1−2+(1/(t+1)))dt=12[(t^2 /2)−t+ln(t+1)]_0 ^1 =12((1/2)−1+ln(2))=6(ln4−1)](Q165619.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}\left(\sqrt[{\mathrm{3}}]{{x}}+\sqrt[{\mathrm{4}}]{{x}}\right)}\:,\:{x}={t}^{\mathrm{12}} \:\Rightarrow{dx}=\mathrm{12}{t}^{\mathrm{11}} {dt} \\ $$$$\:\:\:=\mathrm{12}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{11}} }{{t}^{\mathrm{6}} \left({t}^{\mathrm{4}} +{t}^{\mathrm{3}} \right)}=\mathrm{12}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{{t}+\mathrm{1}}{dt}=\mathrm{12}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({t}+\mathrm{1}−\mathrm{1}\right)^{\mathrm{2}} }{{t}+\mathrm{1}}{dt} \\ $$$$\:\:\:=\mathrm{12}\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}+\mathrm{1}−\mathrm{2}+\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}=\mathrm{12}\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−{t}+\mathrm{ln}\left({t}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:=\mathrm{12}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}+\mathrm{ln}\left(\mathrm{2}\right)\right)=\mathrm{6}\left(\mathrm{ln4}−\mathrm{1}\right) \\ $$
