Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 97057 by bemath last updated on 06/Jun/20

∫_0 ^1 (dx/(√(−ln(x)))) ? [ by Gamma function ]

$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{dx}}{\sqrt{−\mathrm{ln}\left({x}\right)}}\:?\:\left[\:{by}\:{G}\mathrm{amma}\:\mathrm{function}\:\right] \\ $$

Answered by Sourav mridha last updated on 06/Jun/20

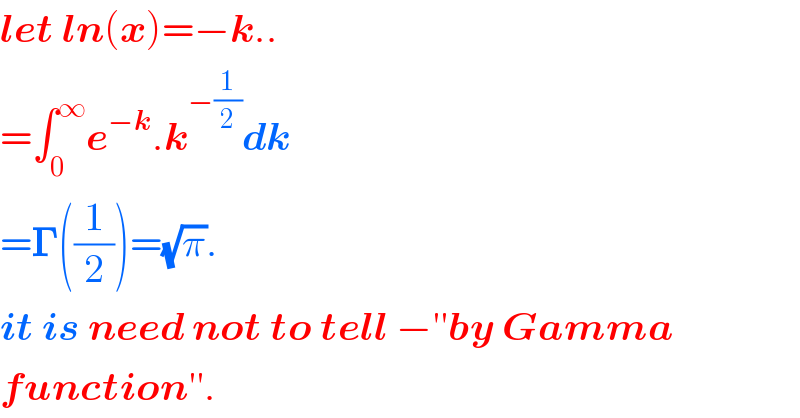
let ln(x)=−k.. =∫_0 ^∞ e^(−k) .k^(−(1/2)) dk =𝚪((1/2))=(√π). it is need not to tell −′′by Gamma function′′.

$$\boldsymbol{{let}}\:\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)=−\boldsymbol{{k}}.. \\ $$$$=\int_{\mathrm{0}} ^{\infty} \boldsymbol{{e}}^{−\boldsymbol{{k}}} .\boldsymbol{{k}}^{−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dk}} \\ $$$$=\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}. \\ $$$$\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{need}}\:\boldsymbol{{not}}\:\boldsymbol{{to}}\:\boldsymbol{{tell}}\:−''\boldsymbol{{by}}\:\boldsymbol{{Gamma}}\: \\ $$$$\boldsymbol{{function}}''. \\ $$

Commented by bemath last updated on 06/Jun/20

yes. thanks

$$\mathrm{yes}.\:\mathrm{thanks} \\ $$

Answered by mathmax by abdo last updated on 06/Jun/20

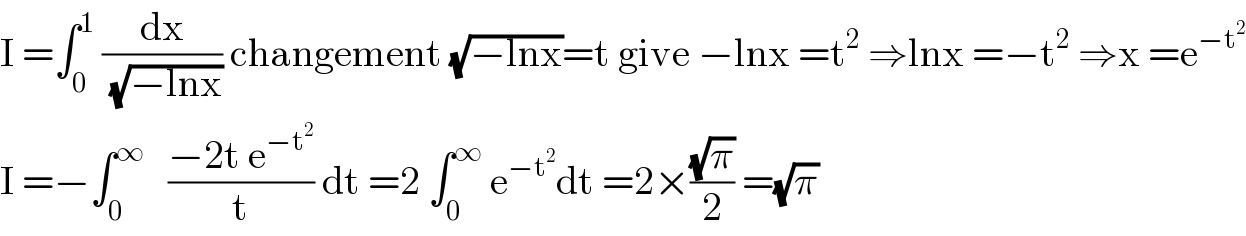
I =∫_0 ^1 (dx/(√(−lnx))) changement (√(−lnx))=t give −lnx =t^2 ⇒lnx =−t^2 ⇒x =e^(−t^2 ) I =−∫_0 ^∞ ((−2t e^(−t^2 ) )/t) dt =2 ∫_0 ^∞ e^(−t^2 ) dt =2×((√π)/2) =(√π)

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\sqrt{−\mathrm{lnx}}}\:\mathrm{changement}\:\sqrt{−\mathrm{lnx}}=\mathrm{t}\:\mathrm{give}\:−\mathrm{lnx}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{lnx}\:=−\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{−\mathrm{2t}\:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } }{\mathrm{t}}\:\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=\mathrm{2}×\frac{\sqrt{\pi}}{\mathrm{2}}\:=\sqrt{\pi} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com