
Question Number 174560 by mnjuly1970 last updated on 04/Aug/22
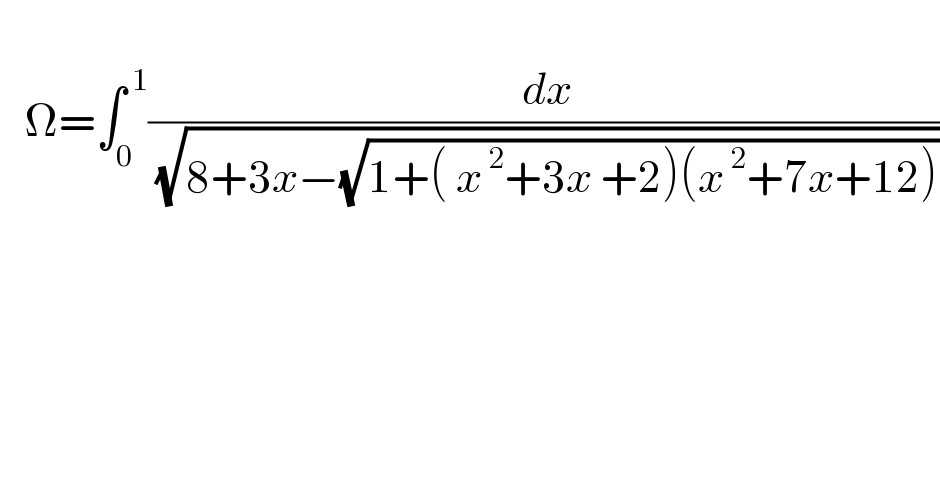
$$ \\ $$$$\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{dx}}{\:\sqrt{\mathrm{8}+\mathrm{3}{x}−\sqrt{\mathrm{1}+\left(\:{x}^{\:\mathrm{2}} +\mathrm{3}{x}\:+\mathrm{2}\right)\left({x}^{\:\mathrm{2}} +\mathrm{7}{x}+\mathrm{12}\right)}}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 04/Aug/22
![1+(x^2 +3x+2)(x^2 +7x+12)=(x^2 +5x+5)^2 x^2 +5x+5>0∀x∈[0; 1] ⇒ Ω=∫_0 ^1 (dx/( (√(−x^2 −2x+3))))= [t=arcsin ((x+1)/2) → dx=(√(−x^2 −2x+3))dt] =∫_(π/6) ^(π/2) dt=[t]_(π/6) ^(π/2) =(π/3)](Q174563.png)
$$\mathrm{1}+\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{12}\right)=\left({x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}>\mathrm{0}\forall{x}\in\left[\mathrm{0};\:\mathrm{1}\right] \\ $$$$\Rightarrow \\ $$$$\Omega=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\:\sqrt{−{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\frac{{x}+\mathrm{1}}{\mathrm{2}}\:\rightarrow\:{dx}=\sqrt{−{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}}{dt}\right] \\ $$$$=\underset{\pi/\mathrm{6}} {\overset{\pi/\mathrm{2}} {\int}}{dt}=\left[{t}\right]_{\pi/\mathrm{6}} ^{\pi/\mathrm{2}} =\frac{\pi}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 04/Aug/22

$${thanks}\:{slot}... \\ $$
Answered by MJS_new last updated on 04/Aug/22
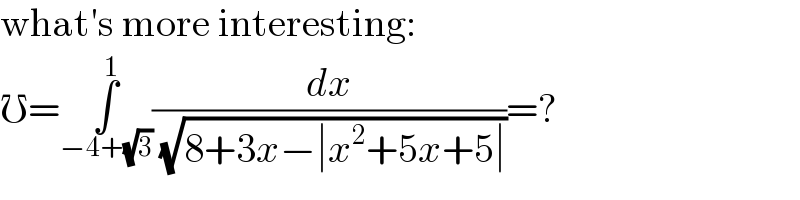
$$\mathrm{what}'\mathrm{s}\:\mathrm{more}\:\mathrm{interesting}: \\ $$$$\mho=\underset{−\mathrm{4}+\sqrt{\mathrm{3}}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\:\sqrt{\mathrm{8}+\mathrm{3}{x}−\mid{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}\mid}}=? \\ $$
Commented by Ar Brandon last updated on 04/Aug/22
![℧=∫_(−4+(√3)) ^α (dx/( (√(8+3x+x^2 +5x+5))))+∫_α ^1 (dx/( (√(8+3x−(x^2 +5x+5))))) ℧=∫_(−4+(√3)) ^α (dx/( (√(x^2 +8x+13))))+∫_α ^1 (dx/( (√(3−2x−x^2 )))) , α=((−5+(√5))/2) =∫_(−4+(√3)) ^α (dx/( (√((x+4)^2 −3))))+∫_α ^1 (dx/( (√(4−(x+1)^2 )))) =[argch(((x+4)/( (√3))))]_(−4+(√3)) ^α +[arcsin(((x+1)/2))]_α ^1 =[ln∣(x+4)+(√(x^2 +8x+13))∣]_(−4+(√3)) ^α +(π/2)−arcsin((((√5)−4)/4))](Q174574.png)
$$\mho=\int_{−\mathrm{4}+\sqrt{\mathrm{3}}} ^{\alpha} \frac{{dx}}{\:\sqrt{\mathrm{8}+\mathrm{3}{x}+{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}}}+\int_{\alpha} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{8}+\mathrm{3}{x}−\left({x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{5}\right)}} \\ $$$$\mho=\int_{−\mathrm{4}+\sqrt{\mathrm{3}}} ^{\alpha} \frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{13}}}+\int_{\alpha} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{3}−\mathrm{2}{x}−{x}^{\mathrm{2}} }}\:,\:\alpha=\frac{−\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:=\int_{−\mathrm{4}+\sqrt{\mathrm{3}}} ^{\alpha} \frac{{dx}}{\:\sqrt{\left({x}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{3}}}+\int_{\alpha} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{4}−\left({x}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:=\left[\mathrm{argch}\left(\frac{{x}+\mathrm{4}}{\:\sqrt{\mathrm{3}}}\right)\right]_{−\mathrm{4}+\sqrt{\mathrm{3}}} ^{\alpha} +\left[\mathrm{arcsin}\left(\frac{{x}+\mathrm{1}}{\mathrm{2}}\right)\right]_{\alpha} ^{\mathrm{1}} \\ $$$$\:\:\:\:=\left[\mathrm{ln}\mid\left({x}+\mathrm{4}\right)+\sqrt{{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{13}}\mid\right]_{−\mathrm{4}+\sqrt{\mathrm{3}}} ^{\alpha} +\frac{\pi}{\mathrm{2}}−\mathrm{arcsin}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{4}}{\mathrm{4}}\right) \\ $$
