Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 156616 by amin96 last updated on 13/Oct/21

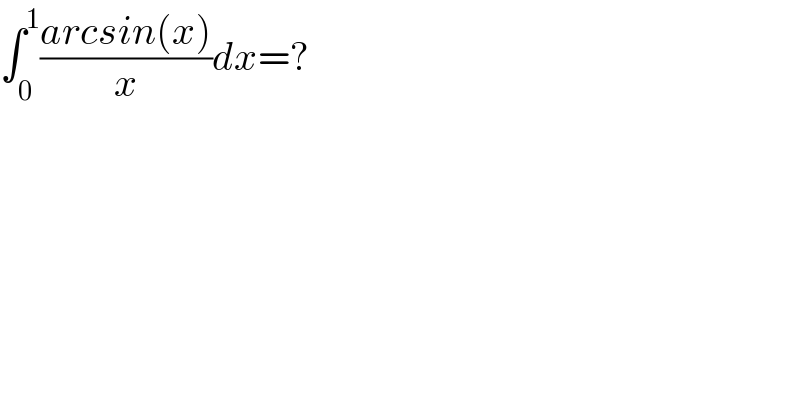
∫_0 ^1 ((arcsin(x))/x)dx=?

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsin}\left({x}\right)}{{x}}{dx}=? \\ $$

Answered by mindispower last updated on 13/Oct/21

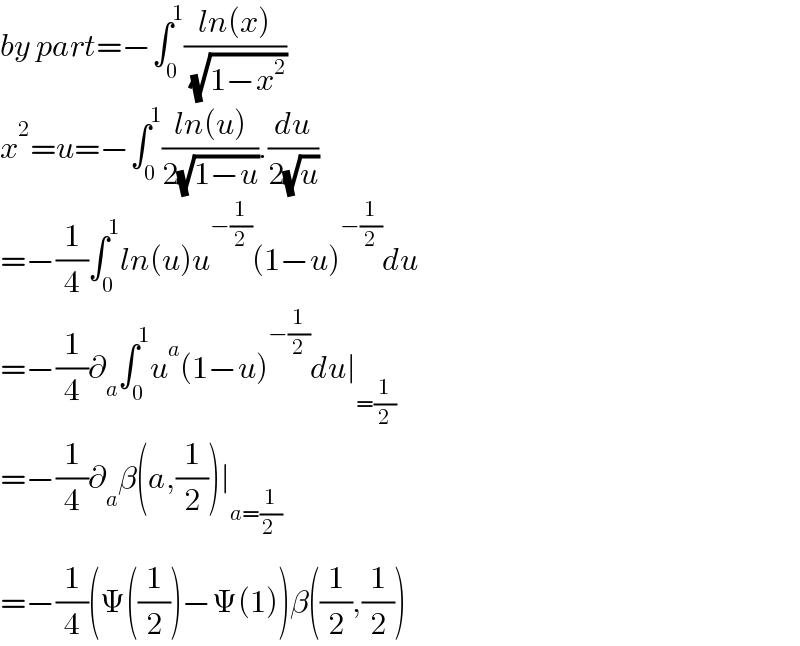
by part=−∫_0 ^1 ((ln(x))/( (√(1−x^2 )))) x^2 =u=−∫_0 ^1 ((ln(u))/(2(√(1−u)))).(du/(2(√u))) =−(1/4)∫_0 ^1 ln(u)u^(−(1/2)) (1−u)^(−(1/2)) du =−(1/4)∂_a ∫_0 ^1 u^a (1−u)^(−(1/2)) du∣_(=(1/2)) =−(1/4)∂_a β(a,(1/2))∣_(a=(1/2_ )) =−(1/4)(Ψ((1/2))−Ψ(1))β((1/2),(1/2))

$${by}\:{part}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}\right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${x}^{\mathrm{2}} ={u}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({u}\right)}{\mathrm{2}\sqrt{\mathrm{1}−{u}}}.\frac{{du}}{\mathrm{2}\sqrt{{u}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({u}\right){u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\partial_{{a}} \int_{\mathrm{0}} ^{\mathrm{1}} {u}^{{a}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du}\mid_{=\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\partial_{{a}} \beta\left({a},\frac{\mathrm{1}}{\mathrm{2}}\right)\mid_{{a}=\frac{\mathrm{1}}{\mathrm{2}_{} }} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left(\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{1}\right)\right)\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Answered by puissant last updated on 13/Oct/21

Q=∫_0 ^1 ((arcsinx)/x)dx IBP ⇒ Q=−∫_0 ^1 ((lnx)/( (√(1−x^2 ))))dx x=sinu→dx=cosudu ⇒ Q=−∫_0 ^(π/2) ((ln(sinu))/(cosu))cosudu ⇒ Q=−∫_0 ^(π/2) ln(sinu)du ∫_0 ^(π/2) ln(sinx)dx=−(π/2)ln2 ∴∵ Q = ∫_0 ^1 ((arcsinx)/x)dx = (π/2)ln2..

$${Q}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsinx}}{{x}}{dx} \\ $$$$\:{IBP}\:\Rightarrow\:{Q}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${x}={sinu}\rightarrow{dx}={cosudu} \\ $$$$\Rightarrow\:{Q}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{ln}\left({sinu}\right)}{{cosu}}{cosudu} \\ $$$$\Rightarrow\:{Q}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinu}\right){du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sinx}\right){dx}=−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\therefore\because\:\:{Q}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arcsinx}}{{x}}{dx}\:=\:\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}.. \\ $$

Commented by amin96 last updated on 13/Oct/21

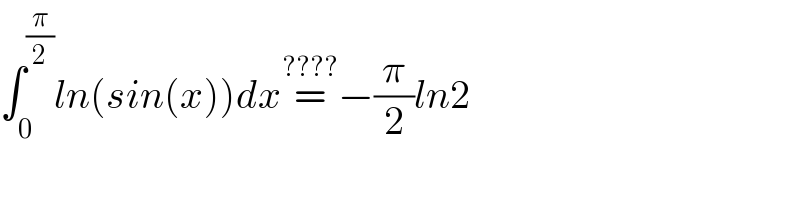
∫_0 ^(π/2) ln(sin(x))dx=^(????) −(π/2)ln2

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}\overset{????} {=}−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}\:\: \\ $$

Commented by puissant last updated on 13/Oct/21

yessssssss sir..

$${yessssssss}\:{sir}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com